数学は数量と厳密な論理に基づいて物事を整理する学問としてはるか昔から発展を続けています。数を扱う代数学と図形を扱う幾何学の基本的な成果は古代ギリシア時代まで遡ります。17世紀以降、力学に端を発して、自然現象の解析に数学の考え方が応用されるようになりました。その中で解析学が生まれると同時に数学全般が飛躍的に発展し、数学は「科学の言葉」としての地位を獲得しました。数学そのものを探究すると同時にそれを応用し、数学を共通の言葉として様々な科学に通じる「理(ことわり)」を明らかにしようとする学問が数理科学です。
数理科学科の3つの特徴

応用も見据えて数学を包括的に学ぶ
数学の基礎が確立された現代では、膨大な理論の系統的な整理が進んでいます。数理科学科が提供する分野には代数学・幾何学・解析学・確率論・離散数学があり、また応用に主眼のある分野として、統計科学・数値計算・最適化があります。これらすべての分野の基礎概念を包括的に学び、さらに現実問題への応用として、データの統計的処理の方法やコンピュータを活用した数値シミュレーションの方法も学びます。関連する様々な分野に興味関心を広げることで、数学の味わいがさらに深まります。

数学の深い理解に基づいて数学を応用する
数理科学科の教育研究の特徴は、数学の既存の結果を単に利用するのではなく、定理の背景やその証明に関する深い理解に基づいて数学に携わることです。このような姿勢によって、「科学の言葉」としての数学を活用し尽くすことが可能になります。さらに、困難に直面した場合でも、新たな数学的手法を開発して問題を解決できます。
論証をたどる力を身につけ、数学的思考を獲得する
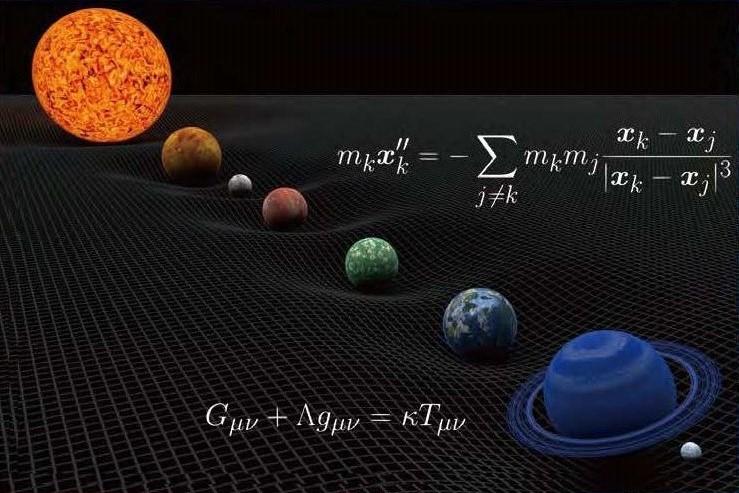
数学を味わうと同時に正しく応用するためには「論理の連鎖」を正確にたどる練習が不可欠です。2年生までに全員が学ぶ極限の概念・微分積分・線形代数によってその基礎を養います。「分かる」とはどういうことなのか、感動を持って再認識できる瞬間が来るはずです。数理科学科は、数学の教育研究を通して、抽象的・普遍的に物事を見ることができ、それに基づいて確実な判断を示せる人材の育成を目指しています。
数理科学科での学び方

古代から存在する「整数」の概念から深い数学の世界を学ぶ
人類の黎明期から使われていた整数は、四則演算を超えた「代数的構造」の研究を通して、深い数学とつながります。岩澤理論のような新しい理論が現代でも創られています。整数の理論を応用すると、例えば、辺の長さがすべて整数となる直角三角形と二等辺三角形の組で、周の長さと面積が等しいものは (相似を除いて)上図のものしかないことが示されます。また、情報社会の基盤を成す暗号理論や符号理論とも深く関わっています。
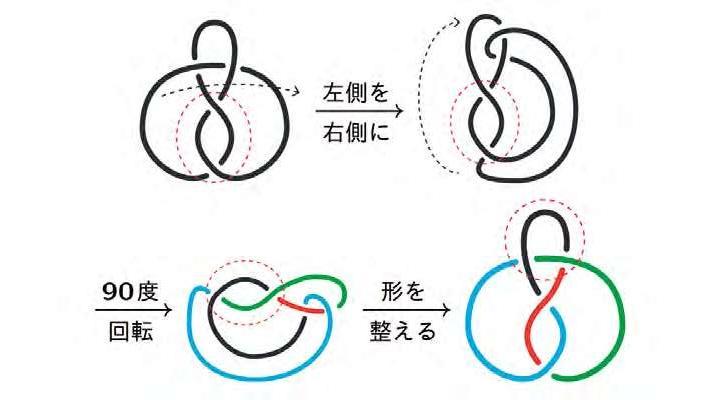
球面の曲がり具合など図形に関するありとあらゆる性質を解き明かす
幾何学とは図形の特徴を数によって表し、その性質を調べる学問です。例えば、平面図形においては、長さ・角度・面積などが特徴を表す数量となります。本学科では、より複雑な図形を対象とし、絡んだ糸を数学的に抽象化した結び目とその絡み具合を表す「不変量」や、球面など表面が曲がった図形の曲がり具合を表す「曲率」などを研究しています。

マクロな解析とミクロな解析で現象を理解する
物事を見るスケールを変えることで、様々な自然現象・社会現象・経済現象をより詳しく解析することが可能になります。例えば、インクや熱の拡散をマクロなスケールで記述する拡散方程式は、インクの粒子や原子一つ一つのランダムな動きの積み重ねとして導出することができます。このような問題で重要な役割を果たす確率論や偏微分方程式論を研究しています。
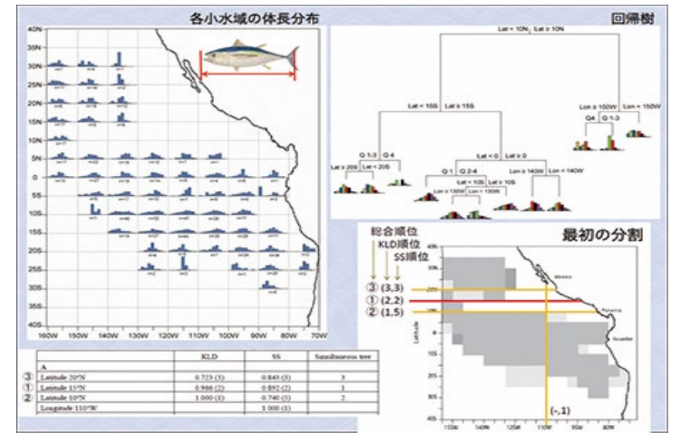
現象を数値で読み解き新しいモデルを構築する
株価の動向や疫病の要因など、私たちの身の回りに起こる様々な現象を理解するための方法論として統計科学があります。統計科学では、データの要約や可視化などの基本的な統計処理から始め、数学的なモデルを駆使して現象の深い理解や意思決定を裏付けます。そのために、データ収集からモデリング、推定アルゴリズム、統計量の挙動の解析、結果の解釈までを系統的に扱います。
在学生インタビュー(過年度)
学習・教育目標
抽象化・普遍化された理論の研究によって、物事の本質にアプローチすることが数理科学の使命であるといえます。そのためには、なにより理論的な基礎の理解が必要となります。数理科学科ではこのような考えのもとに、数学の基礎理論の理解を教育の目標としています。また、データを統計学的に扱うための理論的基礎、コンピュータ計算の基礎原理なども、それぞれの分野における教育の目標となっています。このように理論的な基礎を十分に身につけることこそが、どのように変化する状況にあっても本質的なものを見きわめる力を養うことになると考えています。また、抽象的・普遍的に物事を見ることができ、それをもとに確実な判断を示すことのできる人材の育成が、数理科学科に求められていると考えます。
教育内容
- 本学科には数学専攻と統計学専攻との2コースがあります。
- 数学専攻では、解析学・幾何学・代数学など、純粋数学の諸分野における基礎を学ぶと同時に、それらが自然科学の諸分野に向けてどんな応用を持っているのか、その可能性を追求します。
- 統計学専攻では、数学・統計学を基礎として、工学・社会科学の諸問題を解決する専門家を養成することに重点をおいています。
- 数学専攻では、解析学(特に関数解析、微分方程式論)、代数学、幾何学、数理情報などの学習が主となります。
- 統計学専攻では、確率論、数理統計学、応用統計学、計算機数学、離散数学、計画数学、保険数学、数値解析などを学びます。
進路
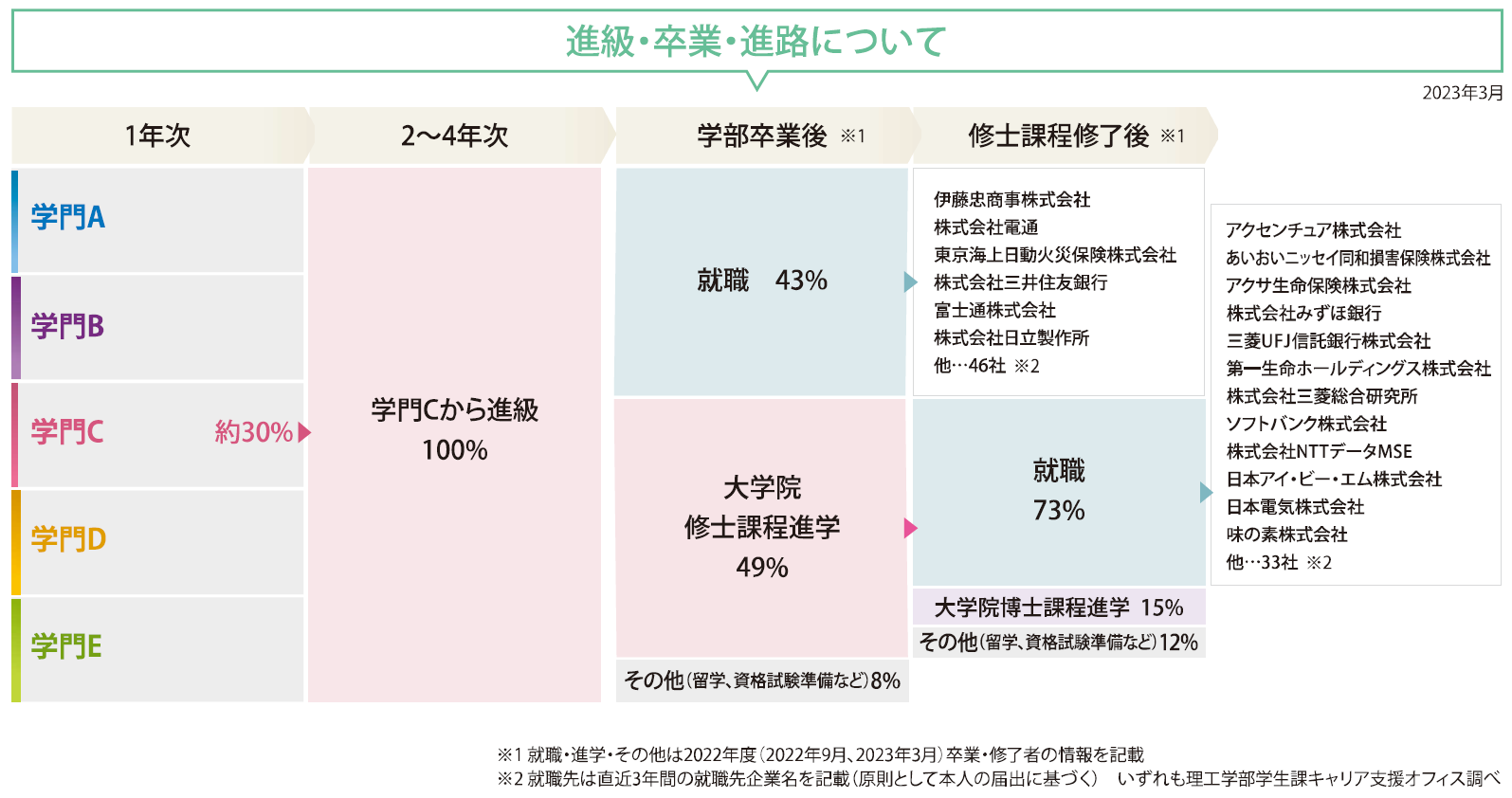
数学的な思考力、分析力は幅広い分野で求められています。企業からの求人は豊富であり、特に金融系、メーカー系(ハードウェア、ソフトウェア)、教育関係への就職が多いです。さらに高度な研究能力を養うため、多数の学生が大学院へ進学しています。



