私は数学の一分野である幾何学を専門にしています。幾何学は広い意味での図形を対象とする数学であり、 まずは個々の対象を直観的に捉えることからスタートします。しかし、そこから一歩踏み出すためには、直観的に捉えた対象を抽象化し、論理的な考察に耐え得る数学的対象に翻訳するという作業が必要になります。
次の図は、正三角形を平面に敷き詰めて得られる模様(タイリングと呼ぶことにします)の一部です。正三角形の一辺の長さを1とすると、このタイリングは、左右に1だけ平行移動しても不変だし、斜めにπ/3の角度で1だけ平行移動しても不変です。さらに、このタイリングは、図に現われるどの直線を軸とした鏡映に関しても不変になっています。

実は、このタイリングは、一つ正三角形△を決め、△の各辺を含む三つの直線を軸とする三つの鏡映で△を繰り返し移していくことによって得られます:
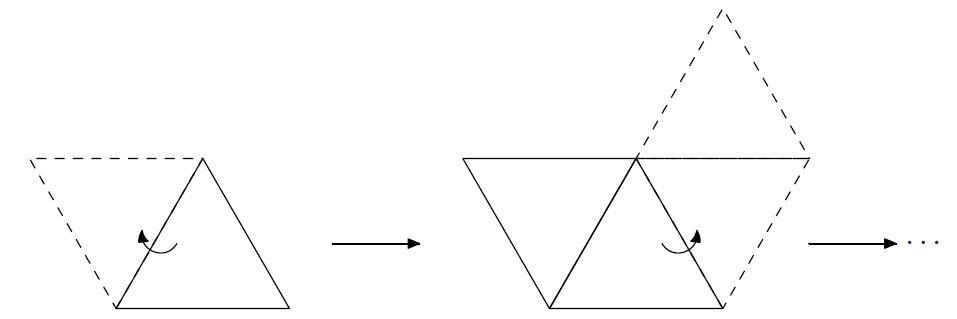
つまり、このタイリングの基本となる図形は一つの正三角形△で、その並び方から感じられる規則性 ― このタイリングの対称性 ― は、三つの鏡映を様々な順序で繰り返し合成して得られる合同変換の集合Gにより記述されていることになります。このGは代数学の対象である「群」の構造をもちます。
平面上で展開される「ユークリッド幾何学」は「与えられた点を通り、与えられた直線と交わらない直線がただ一つ存在する」という平行線の公準を満たしています。次に見る「双曲平面」は、この平行線の公準を満たさない非ユークリッド幾何学のモデルで、複素平面の単位円の内部に

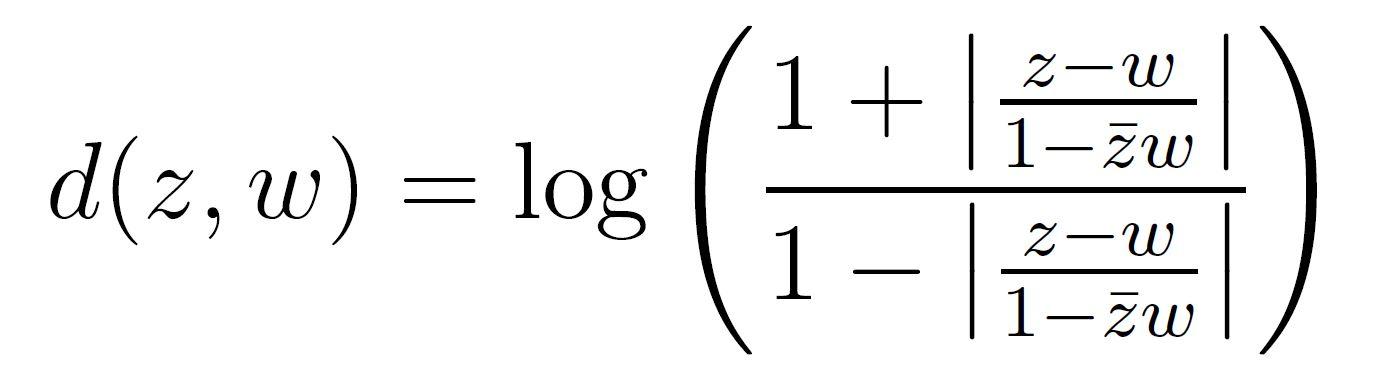
という距離d(・,・)を与えた距離空間です。|wn|→1となるような双曲平面の点列{wn}は、任意にとった双曲平面の点zに対し、d(z,wn)→ ∞を満たします。つまり、双曲平面の縁にあたる単位円周は、双曲平面の住人にとっては、無限に遠いところにある「理想境界」なのです。双曲平面における直線は、その理想境界である単位円と直交する円弧になります。下の図は一つの角がπ/6の双曲正三角形によるタイリングです。(この図からも双曲平面では平行線の公準が満たされていないことがわかります。)
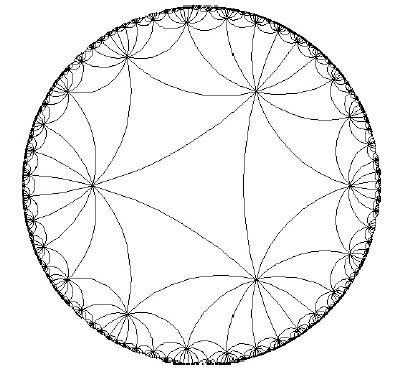
http://aleph0.clarku.edu/˜djoyce/poincare/ より
この図では、双曲平面の中心近くの双曲三角形と縁に近い双曲三角形はずいぶん大きさが違うように見えますが、我々にそう見えるだけで、双曲平面の住人にとってはどの双曲三角形も合同なのです。このタイリングの対称性を表す群G'は、一見すると先ほどのGに似ているのですが、GとG'は、ユークリッド平面と双曲平面の幾何学的性質の違いを反映した、まったく異なる性質をもっています。(例えばGはZ2を有限指数の部分群にもちますが、G'は階数2の自由群を含んでいます。) 対称性を表す群に、それぞれのタイリングの幾何学的性質の違いが鮮明に反映されているのです。
幾何学者にとって、群は空間のもつ複雑な対称性を記述する言葉と言えます。私自身も、群がどのような空間にどのように作用し得るのかを研究をしています。最近、その成果から、多くの群が(それなりによい)作用をする空間を厳しく選ぶ傾向があることが見えてきました。このような性質は「群の剛性」と呼ばれるいささか不思議な性質と関係し、現在、世界中の多くの数学者により活発に研究されています。


