数学は数量と厳密な論理に基づいて物事を整理する学問としてはるか古代から発展を続けています。17世紀以降、力学に端を発して、自然現象を理解するために数学の考え方が本格的に応用されるようになりました。その中で「解析学」という新たな数学の分野が生まれました。 自然現象を調べるにあたって、時々刻々と変化する現象を数式で表現する手段として「関数」という概念が登場します。 例えば、しばしば“さまよう”ような動きを見せる惑星の運動を調べるに先立ち、各時刻における惑星の位置を与える規則があると仮定します。この規則を 𝓊 と表し、時刻 𝓉 における惑星の位置を 𝓊(𝓉) と表します。規則 𝓊 のことを関数といいます。この時点では関数 𝓊 が具体的に何であるか不明ですが、 𝓊 はデタラメに決まるのではなく、何らかの自然界の「法則」に従っていることが予想されます。「法則」を見つけることは物理学の重要な役目です。
惑星の運動を表現する関数 𝓊 が従うべき法則として、例えば「加速度は力に比例する(運動の法則)」というものがあります。 位置の変化率が速度、速度の変化率が加速度です。 関数 𝓊 の条件として「加速度は力に比例する」ことを要請すると、 𝓊 に関するある方程式(常微分方程式)が得られます。この方程式の解 𝓊 を見つけることができて、さらに 𝓊 の性質が詳しく分かれば、惑星の運動が理解できるというわけです。運動の法則とは一見すると異なる法則として「“コスト”を最小にする関数 𝓊 が実際に起こる運動である(最小作用の原理)」というものがあります。すなわち、惑星の運動を表す関数(経路)の候補が無数にある中で、ある候補は“遠回り”するので“コスト”が大きくなり、別の候補は“無駄なく”進むので“コスト”が小さい、という具合になっているとします。この状況で“コスト”を最小にするような関数 𝓊 (経路)を見つければ、惑星の運動が理解できるというわけです。“コスト”が具体的にどのようなものか明らかにすることも物理学の重要な役割です。やや乱暴な表現になりますが、運動の法則と最小作用の原理は数学的に同等であることが示されます。 解析学はこれらの議論を厳密に行うための数学的枠組みを与えます。解析学で最も基本となる概念の1つとして「微分・積分」があります。位置を表す関数 𝓊 から速度や加速度を定式化するためには、まず平均変化率
惑星の運動を表現する関数 𝓊 が従うべき法則として、例えば「加速度は力に比例する(運動の法則)」というものがあります。 位置の変化率が速度、速度の変化率が加速度です。 関数 𝓊 の条件として「加速度は力に比例する」ことを要請すると、 𝓊 に関するある方程式(常微分方程式)が得られます。この方程式の解 𝓊 を見つけることができて、さらに 𝓊 の性質が詳しく分かれば、惑星の運動が理解できるというわけです。運動の法則とは一見すると異なる法則として「“コスト”を最小にする関数 𝓊 が実際に起こる運動である(最小作用の原理)」というものがあります。すなわち、惑星の運動を表す関数(経路)の候補が無数にある中で、ある候補は“遠回り”するので“コスト”が大きくなり、別の候補は“無駄なく”進むので“コスト”が小さい、という具合になっているとします。この状況で“コスト”を最小にするような関数 𝓊 (経路)を見つければ、惑星の運動が理解できるというわけです。“コスト”が具体的にどのようなものか明らかにすることも物理学の重要な役割です。やや乱暴な表現になりますが、運動の法則と最小作用の原理は数学的に同等であることが示されます。 解析学はこれらの議論を厳密に行うための数学的枠組みを与えます。解析学で最も基本となる概念の1つとして「微分・積分」があります。位置を表す関数 𝓊 から速度や加速度を定式化するためには、まず平均変化率
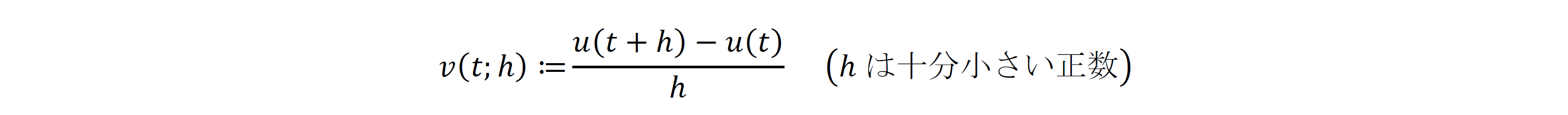
に着目しますが、𝒽 の取り方の不定性を排除するために、𝒽 を0に近づけたときに 𝓋(𝓉;𝒽) が限りなく近づくであろう値をもって速度 𝓊'(𝓉) を定義します:
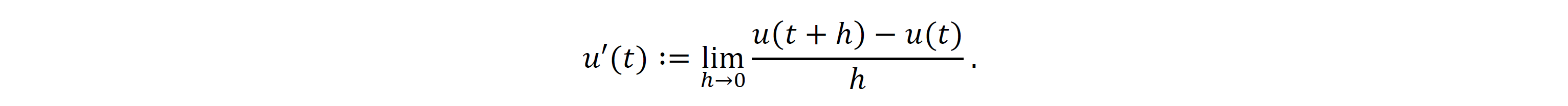
これが「微分」と呼ばれる概念です。𝓊'(𝓉) が存在するかどうかは非自明であり、「限りなく近づく(極限)」の厳密な定義とともに関数の微分に関する様々な事柄が整理されています。また解析学では、運動の法則から帰結されるものを含む一般の常微分方程式を解くための理論も整備されています。すなわち、常微分方程式の初期値問題の一般形(高階の常微分方程式もこの形に変形される)
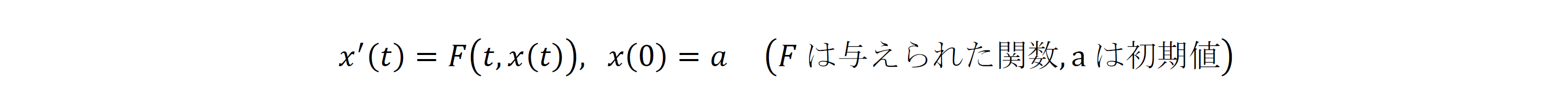
に対して、解の存在と一意性を証明することが可能です。微分方程式の解の存在を示す強力な方法として「近似解の構成とその収束」があります。例えば、𝓍'(𝓉)=F(𝓉,𝓍(𝓉))の近似として次のものが知られています: 𝒽 を正定数、 𝓀=0,1,2…、𝓉𝓀=𝓀𝒽 として
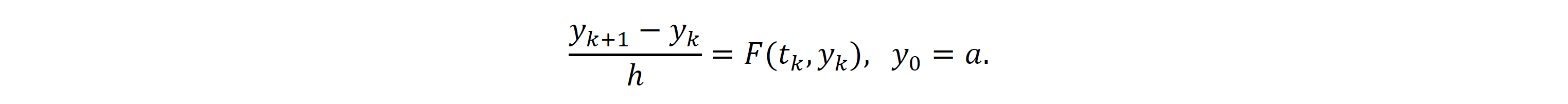
これは連続な時間変数を刻み幅 𝒽 で離散化し、微分 𝓍'(𝓉) を時間幅 𝒽 の平均変化率で近似したものになります。𝓀=0 から始めれば、四則演算によって直ちに𝓎0, 𝓎1,𝓎2 … が得られます。各 𝒽 に対して近似解のグラフ{ (𝓉𝓀,𝓎𝓀) | 𝓀=0,1,2,…} の隣接点同士を線分で結ぶことによって折れ線関数 𝓍𝒽 が得られます。ここで 𝒽 を0に近づけると、関数 𝓍𝒽 の“折れ具合”はどんどん細かくなり、その極限において 𝓍𝒽 は何らかの滑らかな関数 𝓍 に“収束”し、 𝓍 は真の解になっていることが期待されます。この予想を厳密に証明することが可能です。そのためには、数列の収束の概念を一般化した「関数列の収束」(上の例では折れ線関数 𝓍𝒽 の列の収束)について詳しく調べる必要があります。「積分」は、曲がった図形の面積の概念に関連していると同時に、微分演算を元に戻す演算でもあり、様々な場面で非常に重要な役割を担っています。最小作用の原理で述べた「関数(経路)の持つ“コスト”」は、例えば次のような積分で与えられます:
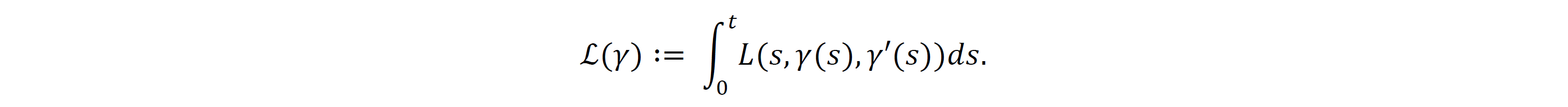
ただし L は既知の関数、 γ は経路を表す関数になります。ℒ は「考え得る経路 γ の全体、すなわち関数の集合上で定義された関数」という意味で「汎関数」とも呼ばれます。ℒ を最小にするような関数(すなわち“無駄”のない経路)を見つける問題は、例えば数直線上で定義された関数 𝓎=𝓍4−4𝓍3+𝓍2+3𝓍−1 の最小点を求める問題の一般化と見ることができます。 ℒ の定義域は数直線ではなく関数の集合になっているため、問題は格段に難しくなります。ここでも「関数列
の収束」の概念が非常に重要な役割を果たします。
上記以外にも様々な現象に対応する微分方程式が導出されており、これらを解くために解析学がどんどん発展しています。また、力学以外の様々な問題においても「“コスト”の最小化」という考え方の有用性が明らかになっており、解析学において「変分法」と呼ばれる理論が発展しています。問題に応じた適切な関数の集合を設定し、その集合における関数列の収束やその他の諸性質を明らかにすることが解析学の基礎となります。そしてこれらの枠組みを駆使して現象を解明することも解析学の重要な役割になります。
本稿を通して、解析学という比較的新しい数学の一分野の背景や役割について垣間見ていただければ幸いです。
上記以外にも様々な現象に対応する微分方程式が導出されており、これらを解くために解析学がどんどん発展しています。また、力学以外の様々な問題においても「“コスト”の最小化」という考え方の有用性が明らかになっており、解析学において「変分法」と呼ばれる理論が発展しています。問題に応じた適切な関数の集合を設定し、その集合における関数列の収束やその他の諸性質を明らかにすることが解析学の基礎となります。そしてこれらの枠組みを駆使して現象を解明することも解析学の重要な役割になります。
本稿を通して、解析学という比較的新しい数学の一分野の背景や役割について垣間見ていただければ幸いです。




