皆さんは統計学に対してどのようなイメージを持っているでしょうか。私が統計学を研究していると伝えたときの相手の反応はまさに多種多様です。アメリカ人の会計士には「統計学は人を騙すための道具だ」と面と向かって言われましたし、「では測度論が必須ですね」という知的な返答をする人もいます。ある統計学者は、小学校の恩師に「それでは鶏を飼育しているのですか?」と、とうけい違いの返答をされたという逸話もあります(こういった話を作るような方ではないのできっと実話です)。最後のものは例外ですが、とにかく統計学の持つイメージは研究者の間でさえ大きく異なり、またここ数年のCovid-19のニュースによっても一般のイメージに変化があったと推測されます。「多面性」がここまで顕著な研究分野は他にもあまり例を見ないのではないでしょうか。
私は最近、統計学の中でも、特にデータの持つ幾何学的な特徴に着目した解析手法を研究しています。古くから研究されている例は方向統計学であり、円周上や球面上に分布するデータを扱います。風向きなどの方向のデータや、地球上の分布データなどがその例です。一方、近年は扱うデータの大規模化、多様化が進み、また解析手法に機械学習も加わり、より複雑な幾何学的構造をもつデータを扱う研究が盛んとなっています。
その中で、私はLondon School of EconomicsのWynn教授との共同研究において、データのもつ「曲率」に着目した新しいデータ解析手法を提案しました。具体的には、まず空間に分布するデータ点の近いもの同士を結んで「近接グラフ」を構成し、そのグラフ上を通る最短経路長でデータ点間の「基本」距離を定義します。この距離自体は、データが多様体(球面やトーラスなどのように「滑らかさ」をもった幾何学的集合)上に分布するときに、その多様体上を通る最短経路(測地線)長の近似となることから、「多様体学習」とよばれる機械学習手法でよく用いられるものです。
我々の手法は、この基本距離をさらに解析精度が向上するような別の距離に変換します。その際には、
(1) データの分布している距離空間の「曲率」が単調に変化するように距離を変化させ、さらに、
(2) 一般には曲率が定義できないような距離への変換でさえも、「計量錐」とよばれる空間に埋め込むことにより、単調な曲率の変化を相対的に可能にする、
ということを提案しました。ここでいう「曲率」はCAT(k)とよばれるもので、近接グラフのような一般の測地距離空間においても曲率を扱えるようにGromovらによって1980年代に提案されたものです。提案した手法はイギリスの地域ごとの降雨量データの解析に応用され、年間の降雨量の「幾何学的な」分散が近年急激に拡大していることが確認されました。これは従来の分散を用いた場合には検出されなかった現象です。
統計学においては、データを入手し、それを解析する手法を開発し、その手法の精度、妥当性を理論的に評価する、もしくは逆に理論をもとにしたアイデアで解析手法を作成します。そして、実際にデータを解析し、その結果を考察するところまで含めると非常に広範なプロセスとなります。その全体を手の届く範囲で実行し、また全体像を俯瞰し設計することができる、私にとってはそれこそが統計学の最大の魅力だと最近は感じています。
私は最近、統計学の中でも、特にデータの持つ幾何学的な特徴に着目した解析手法を研究しています。古くから研究されている例は方向統計学であり、円周上や球面上に分布するデータを扱います。風向きなどの方向のデータや、地球上の分布データなどがその例です。一方、近年は扱うデータの大規模化、多様化が進み、また解析手法に機械学習も加わり、より複雑な幾何学的構造をもつデータを扱う研究が盛んとなっています。
その中で、私はLondon School of EconomicsのWynn教授との共同研究において、データのもつ「曲率」に着目した新しいデータ解析手法を提案しました。具体的には、まず空間に分布するデータ点の近いもの同士を結んで「近接グラフ」を構成し、そのグラフ上を通る最短経路長でデータ点間の「基本」距離を定義します。この距離自体は、データが多様体(球面やトーラスなどのように「滑らかさ」をもった幾何学的集合)上に分布するときに、その多様体上を通る最短経路(測地線)長の近似となることから、「多様体学習」とよばれる機械学習手法でよく用いられるものです。
我々の手法は、この基本距離をさらに解析精度が向上するような別の距離に変換します。その際には、
(1) データの分布している距離空間の「曲率」が単調に変化するように距離を変化させ、さらに、
(2) 一般には曲率が定義できないような距離への変換でさえも、「計量錐」とよばれる空間に埋め込むことにより、単調な曲率の変化を相対的に可能にする、
ということを提案しました。ここでいう「曲率」はCAT(k)とよばれるもので、近接グラフのような一般の測地距離空間においても曲率を扱えるようにGromovらによって1980年代に提案されたものです。提案した手法はイギリスの地域ごとの降雨量データの解析に応用され、年間の降雨量の「幾何学的な」分散が近年急激に拡大していることが確認されました。これは従来の分散を用いた場合には検出されなかった現象です。
統計学においては、データを入手し、それを解析する手法を開発し、その手法の精度、妥当性を理論的に評価する、もしくは逆に理論をもとにしたアイデアで解析手法を作成します。そして、実際にデータを解析し、その結果を考察するところまで含めると非常に広範なプロセスとなります。その全体を手の届く範囲で実行し、また全体像を俯瞰し設計することができる、私にとってはそれこそが統計学の最大の魅力だと最近は感じています。
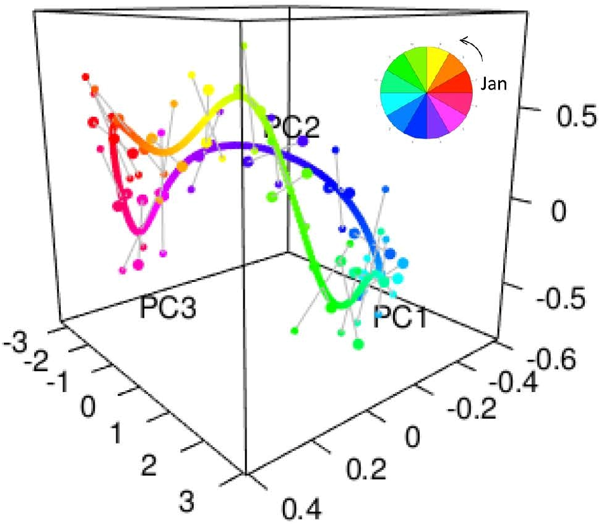
図1:イギリスの85年分の降雨量の年周期構造
主成分分析と呼ばれる手法で3次元に視覚化している。ループの各点が85年分のある日(例えば1月1日)のデータ平均を表し、「ひげ」はデータのばらつきの方向を表している。データが幾何学的構造を持つことが見て取れる。
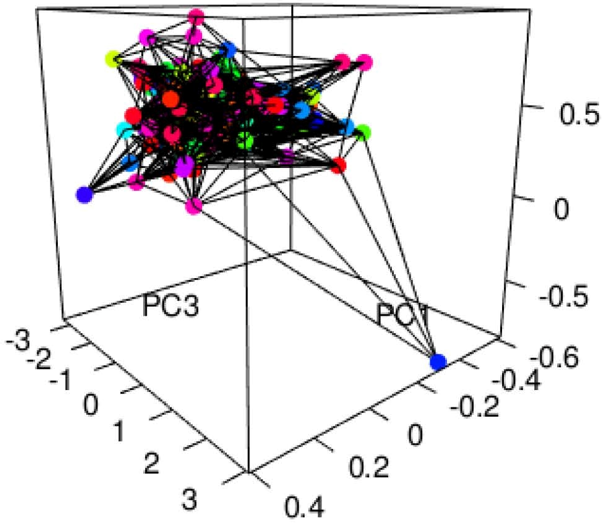
図2:1986年のデータをもとに提案手法で作成した距離グラフ
このグラフをもとにして1986年の365日のデータの幾何学的分散を計算する。ここでの点の色はFréchet関数とよばれるものの値で図1の色とは関係ない。
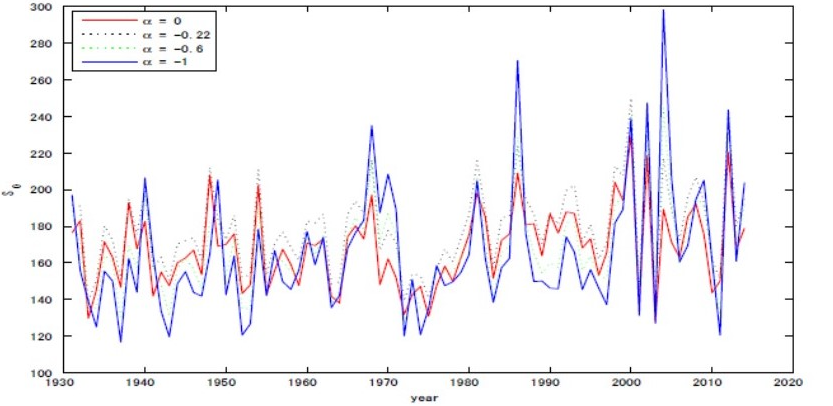
図3:85年分の幾何学的分散の変動
各年の降雨データに対して図2のように構成されたグラフをもとに計算した幾何学的分散の85年分の時系列データ。提案手法(青線)では近年になるにつれて分散が大きくなり、年ごとの変化も拡大する傾向がみられる。この傾向は従来の分散を用いた場合(赤線)ではほぼ確認できない。



