数学世界の広がり
幾何学的着想から整数論の予想問題に取り組む坂内さんは、
高校2年までアメリカで過ごした帰国生だ。
その高校時代に数学に魅せられ、今では数学的思索が趣味になってしまったという。
数学の中に社会や人との関わりを良い方向に向かわせる力を見いだしてきた坂内さんは、
開かれた数学を目指している。
坂内 健一 / Kenichi Bannai
代数多様体のL 関数の特殊値にまつわる予想を背景に、ポリログなどの数論幾何的対象を用いて、抽象的な理論と具体的な特殊関数との関係についての研究を進めている。2000 年、東京大学大学院数理科学研究科博士課程修了。2001 年、名古屋大学大学院多元数理科学研究科助手。名古屋大学在職中、2005 ~ 07 年にフランスのÉcole Normale Supérieure に日本学術振興会海外特別研究員として滞在。2008 年に慶應義塾大学理工学部に専任講師として着任、2012 年より准教授。
研究紹介
今回登場するのは、数学の一分野である整数論において、
数論幾何的手法を用いて未解決の予想問題に取り組む坂内健一准教授です。
数学の予想問題に新たな進展をもたらす
数学的論理体系と直感的思考を統合
人は論理と直感を組み合わせながらさまざまな課題に対応してきた。その直感、たとえば点や線などの幾何学的な図形を見たときに感じる直感を整数論の分野に活かす手法、それが数論幾何である。この数論幾何を用い、整数の性質を扱う整数論の問題に立ち向かう坂内准教授を訪ねた。
数論幾何に内在する理論と直感の絶妙なバランス
「数学の問題を解くときに問題を絵に描いたり、提示された図形に補助線を加えたりすることで直感が働き、問題が簡単に解けた、という経験があったりするかと思います。この図形に代表される幾何学の概念を使い、整数論の課題に取り組むのが数論幾何です」と、坂内さんは自らの研究分野について話す。
幾何学の概念とはどういうことだろう。x2+y2=1 という方程式の有理数解を全て求める問題を例に説明しよう。もちろん、式を一生懸命にいじってこの問題を解くこともできる。しかし、この方程式が平面上に描く半径 1 の単位円を考えると問題はずっと見通しが良くなる(図 1)。(x,y)=(−1, 0)はこの方程式の有理数解である。点(−1, 0)を通る直線を 1 つ考えると、この直線は点(−1,0)以外に単位円ともう 1 点だけで交わる。この直線の傾きが特に有理数であれば、新たに与えられた交点は方程式の有理数解を与える。逆に方程式の有理数解を与えると、点(−1, 0)を通り傾きが有理数の直線が得られる。すなわち、方程式の有理数解は、傾きが有理数の直線と 1 対 1 に対応している。
このような幾何学的な考え方を取り入れた数論幾何は、数の性質を研究する整数論とともに発展してきた。整数論は数学の中でも長い歴史があり、整数の素朴な問題を考える上でも、背後には高度に積み重ねられた論理体系が存在する。応用も広く、最近では暗号や認証技術に活用されている。整数論の問題への 1 つのアプローチが数論幾何で、多くの問題解決への貢献が期待されている。実際、数論幾何の手法はフェルマーの最終定理やモーデル予想(*1)の証明に使われてきた。
「私がテーマとして取り組んできたのが “ポリログ”という幾何学的な対象です。ポリログにはいくつもの整数論的に重要な量を統一的に捉える力があります。数学の予想問題には、一見すると関係なさそうな 2 つの量の関係を明らかにするという問題が多数存在します。そのような問題に対し、その双方を統一的に説明できる上位の概念を提示できれば、両者の関係の解明に一歩近づけます。ポリログはその架け橋的役割を担えるのです」。
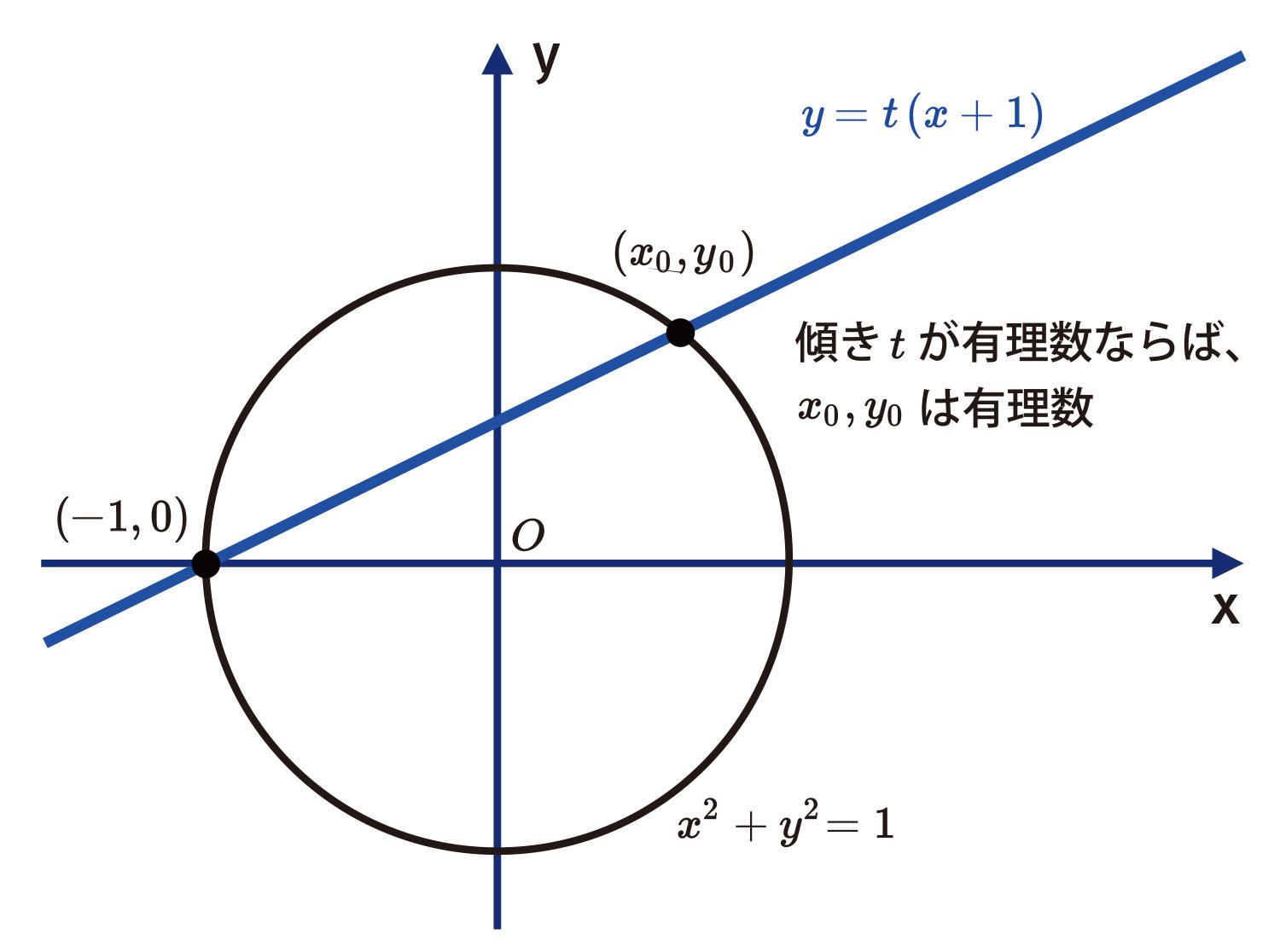
図 1 幾何を使って整数論の問題を解く
方程式 x2+y2=1 の有理数解は、点(−1, 0)を通り傾きが有理数の直線と1対1に対応している。このように、方程式を円と見て図形的に考えると、問題の見通しが良くなる。
問題の本質を捉えることで重要な量の関係を解き明かす
坂内准教授が取り組むポリログは、“幾何学的な対象” の一種である。その概念を説明するため、ここでは “幾何学的な対象” を “図形” と読み替えてみよう。一般に図形があれば、その図形から「面積」や「頂点の数」など、様々な量を導きだすことができる。したがって、比較したい整数論的に大事な量が複数あった場合、これらの量を内在する図形を見つけることができれば、もともとの量を同じ図形の構成要素として捉えることで、異なる量を関係づける数式などを見いだすことができる。ポリログは、整数論的に大事な量を内在的に持っている図形なのである。
「たとえば、A という性質や量をどんどん抽象化したら、シンプルな図形で表せたとします。次に A とは全く違って見える B という性質や量を同じ手法で抽象化します。それが A と同じシンプルな図形で表せた場合、A と B の見た目はバラバラですが、本質的な部分で両者は同じであり、A と B を統合するルールの存在を期待することができるのです」。このような抽象化によって得られる幾何学的な対象を、数論幾何の発展に大きく貢献したグロタンディーク(*2)は“モチーフ(Motive)” と呼ぶ。ポリログは、数論幾何の重要な概念であるこのモチーフの一例である(図 2)。
「グロタンディークが使うモチーフという言葉は、実は画家セザンヌ(*3)の絵画評から引用されています。セザンヌはうつろい行く光と影で描写する印象派から距離を置き、実際の絵画対象(モチーフ)を確実に捉えるという独自の絵画様式の確立に尽力したそうです。表面的な事象ではなく本質を捉えるのが、数論幾何のモチーフです」。
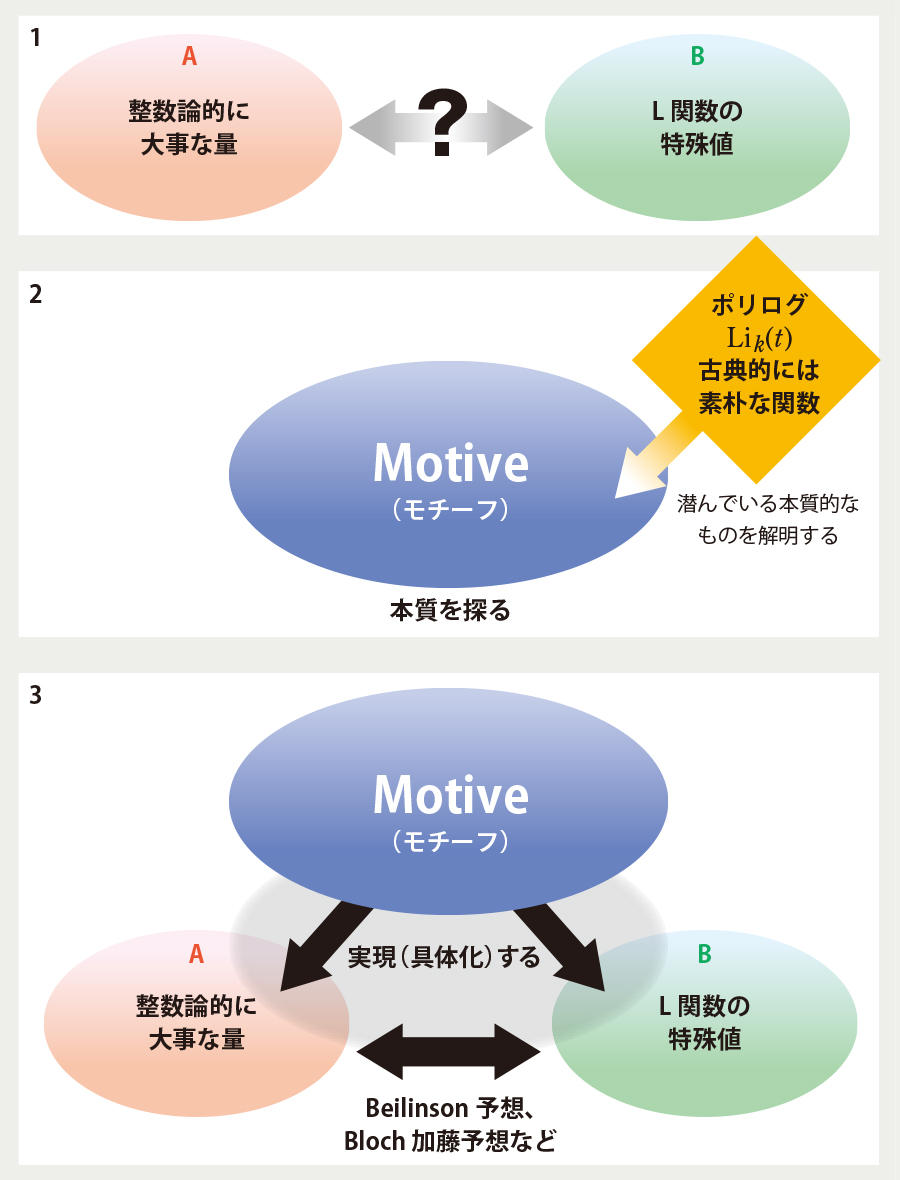
図 2 ポリログのはたらき
(1)「整数論的に大事な量」と「L関数の特殊値」という一見まったく関係のない2つの事象がある。(2)ポリログ関数を抽象化して得られた、この2つの事象の上位にある Motive(モチーフ)を使って、その背景にある本質的な関係を探る。(3)Motive を経由することで、無関係と思われた2つの事象の関係性を示すことができる。その関わりを通して、Beilinson 予想や Bloch 加藤予想などの問題の解決が導かれる。
仲間との共同研究を通し数学の予想問題の解決に挑む
研究内容の奥深さに対して坂内さんがテーマとしてポリログを選んだ理由はシンプルでわかりやすい。
「一番の理由は、ポリログの素朴さにひかれたからです」と坂内さんは微笑む。一般に数学者といえば、研究に没頭する世捨て人的な印象が色濃い。つい孤高を愛する数学者をイメージしてしまうが、実際の状況は必ずしもそうではない。
「高校などで数学の問題を解くときの感覚から、数学の研究は 1 人で孤軍奮闘という印象があるかもしれません。しかし実際のところ数学は、世界中の数学者と様々な考えを議論することを通して研究を進めていく、非常に国際性の高い分野です。私の最近の一連の研究も、ドイツ・レーゲンスブルグ大学の G. Kings教授と共同で行っています。今私の研究室でも、各人それぞれのテーマを持ちながらもお互い議論し合って勉強や研究を進めています。仲間がいるという状況を楽しみつつ、そのメリットを最大限活用しています」。
坂内さんは、ポリログの発展が問題の本質解明に役立つ重要な鍵になると考えている。なにより、様々な性質や量の抽象化を通して統一的なルールを見出すという発想に、未解決の予想問題に対する美しい解法を提供する可能性を見ているのである。
どちらも長らく数学上の未解決問題であったが、モーデル予想は 1983 年にゲルト・ファルティングス(Gerd Faltings)が、フェルマーの最終定理は 1995 年にアンドリュー・ワイルズ(Andrew Wiles)が解決した。
アレクサンドル・グロタンディーク(Alexander Grothendieck)。フランス高等科学研究所(IHÉS)の創始者メンバーである。代数幾何の基盤に可換環論をはじめとして多くの数学的手法を持ち込み豊かな視点を持たせることで、数学全般に革命的な進歩をもたらした。
インタビュー
坂内健一准教授に聞く
『風の谷のナウシカ』に出会って日本に
戻ることを決意
子ども時代をアメリカで過ごされたとのことですが、いつ頃からですか?
2歳からです。私の両親はともに数学者で、父がアメリカのオハイオ州立大学から呼ばれたことをきっかけに、家族全員で渡米しました。1970年代前半のことです。以後、幼稚園の2年間を除いてアメリカにいて、高校2年の2学期の初めに日本に戻ってきました。
高校2年までアメリカにいて、そのままアメリカで進学という
選択肢はなかったのですか?

実は日本に戻ることが決まったとき、すでに飛び級でアメリカの複数の大学から入学許可をもらっていました。1980年代後半、世界が日本の急速な発展に脅威を感じていた時期です。当時、アメリカ人の多くは日本を、年中無休で機械のように働く人々の国と考えていました。私自身、テレビで繰り返し放映された社員全員がそろってラジオ体操をする日本人の姿を見て、全体主義的な国に行くのか、と悲壮感を覚えたものです。
そんなとき、宮崎駿の『風の谷のナウシカ』に出会いました。人間世界とは異なる生態系が映像として見事に描写されていて、このような世界観を生み出す創造力に圧倒されました。これをきっかけに日本に対する興味が深まり、一度日本に戻ってみようという気持ちになりました。
世の中の広い分野で役立つことを知り
数学に興味を持つ
数学に興味を持ったきっかけは?
数学に本格的に興味を持ったのは高校に入ってからでした。当時はやってみたいと思うことがたくさんありました。アインシュタインの相対性理論などの話を聞きかじって物理を勉強してみたいと思ったり、生態系のモデリングの理論を勉強してみて、人間社会についてもうまくモデリングできたらいいなあと思ったり、人間よりも優れた人工知能(AI)を作って友達になってみたいと考えたり、自然言語よりも正確に多くの情報を伝える言語を作ってみることができないかと考えてみたり、理想的な社会制度を立案することで世界平和を達成できたらいいなあと考えたり、映画の台本や小説を書いてみたいと思ったり、とにかく将来、何でもかんでもやりたいと思っていました。やることを限定することはもったいなく理不尽に感じ、何とかならないものかと考えていました。そんなとき、数学がいいかも、と思える出来事に遭遇したのです。
そのきっかけは化学の授業でした。化学反応による物質の濃度変化の計算に、ある微分方程式が現れたのです。それは数学の授業で計算したばかりの方程式で、その時は何とも思いませんでした。しかし、その直後に受けた生物学の大学講義でも、生態系のモデルで動物の個体数を計算するときに、全く同じ微分方程式を解くことになりました。あれ?と思いつつ、さらに経済学の授業で全く同じ微分方程式が利用され、数学の1つの抽象的な微分方程式が、幅広い分野で具体的な意味を持って使われている様子を目の当たりにしたのです。何をするにも数学は使えると思いました。
その思いは、ヘルマン・ヘッセの『ガラス玉演戯』(※)を読んでから、さらに膨らみました。この小説は架空の未来の世界の物語で、数学を始めとして物理化学法則、音楽、詩や芸術などを全て統合して作られた「ガラス玉演戯」と呼ばれる知的芸術遊戯の名人の伝記、という形で書かれています。数学を究めることができれば、化学・生命現象や経済学だけでなく、音楽・文学や芸術までをも全て捉えることができる!と思えるようになったのです。
数学が多分野で使われていることに気付かれたとのことですが、
実際に数学を研究されている今、どう思いますか?

数学には事物を抽象化し、その本質を抜き出す力があります。複雑さを増している現代社会でこそ、数学の抽象化の力が活用できると感じます。様々な価値観の人がいるとき、表面的な差が大きく歩み寄るのが難しく感じることもあるかと思います。しかしながら、全員が達成したいことを十分に考え抜くと、実はやりたいことは本質的には変わらないことに気がつきます。具体的な手段や個別の事情に固執しすぎて共通点がなさそうな場合にも、問題を正しく抽象化して捉えると、同じ土俵に立つことができ、どの解決策が良いかについて冷静に議論できると思います。
数学自身は主に方程式や幾何的図形などの対象を扱いますが、抽象化をはじめとする数学の問題解決の考え方自体は、実社会でも非常に貴重な道具になるのではないかと再認識するようになりました。
今後、私としては、数学の潜在力を存分に発揮させるために、抽象化をはじめとする数学の様々な問題解決手法を習得した人材をどんどん社会に送り出したいと考えています。それにより、例えば縦割りの弊害で悩む組織などで、組織としての目的の本質的な部分を正しく抜き出して、統一した方向性を生み出すことを期待しています。 だからこそ、学生さんには個別の具体的な問題だけでなく、抽象数学もきちんと学んでほしいと思っています。具体的な問題は裏を返せば、結局、応用範囲が狭いですし、個別の事情が複雑に絡むことから問題としても難しいことが多いのです。最初は取っ付きにくいかもしれませんが、抽象数学の明快さと応用範囲の広さは壮観です。
(※)ガラス玉演戯:ドイツの作家ヘルマン・ヘッセ(Hermann Hesse)の著作。
学生や家族にも数学と同じように愛情を持って接する
研究とは別に、何か息抜きにしていることはありますか?

昔から妻と過ごす時間はとても楽しみでしたが、2年ほど前に娘が生まれ、家族との時間がさらに充実したものになりました。ただ、その時間が数学の研究と切り離された時間という感覚はあまりないですね。実は最先端の数学を研究しているときも、学生と接しているときも、そして娘と遊んでいるときも、すべて同じような頭の使い方をしていると感じています。数学と愛娘を同列に扱うと一見冷たい親のように見えてしまうかもしれませんが、私としては数学的対象にも娘に対するときと似たような愛情を抱いているのだと思います。
人との向き合い方というか、関係の築き方について、その本質を考えることが楽しくなって、今ではこうした抽象化というか、数学的思索ともいえる視点を持つことが趣味みたいな感じになっています。
その一方で、現実や具体的な事象を無視した安易な一般化には気を付けなくては、と思います。例えば「人間はこう育てるべきだ」と、どこぞの誰かが言ったことを深く理解せずに聞きかじり、状況を踏まえずに強引に持ち込むといったことです。抽象論を持ち込んで議論することに抵抗がある人が多いのは、あまりにも安易な一般化がはびこっているからではないかと思います。数学の抽象論を利用するときには、問題となる個別の場合に適用可能か、厳しく確かめます。このように、個別の問題の状況をきちんと把握して、考えている抽象論がその場合に適用可能かどうかを常に意識しながら考えていく癖は、とても大切だと思います。
慶應義塾大学の良いところとは、どんなところだと思われますか?
最初に、学生がとても元気だと思います。2007年のフランス滞在中に、ケンブリッジ大学と慶應義塾大学の共催で開かれたUK-Japan Winter Schoolという整数論の研究集会に参加したとき、慶應の学生さんにとても良い印象を持ちました。
また、多くの大学では数学は理学部の中にあり、私がいた東京大学や名古屋大学はさらに数学だけの独立した大学院で、他の学部から離れていたように感じました。でも、慶應では数理科学科は理工学部の中にあり、工学系の学科とも接点を持つことができます。他学科の教員と議論する機会も多く、理学と工学との相乗効果があると思います。元気のいい学生が多く、のびのびとした発想力にあふれているのも、こうした環境があるからかもしれませんね。
どうもありがとうございました。
◎ちょっと一言◎
学生さんから
●最先端の数学を研究されているのに数学者然としたところが全くなく、学生の素朴な疑問や興味にもちゃんと向き合い、面白がってくれる自由闊達な雰囲気が魅力です。授業にも熱心で、僕らに数学の楽しさを気付かせてくれます。行き詰まったときには、さりげなくヒントをくださる優しさもあります。
●新しいもの好きで、気になるものがあれば実際に確かめに行く行動力もあります。先日も電子白板を試すためにメーカーのショールームまで出かけられ、その感想を僕らに熱く語っていました。自分の興味を隠さずに話し、面白いものは面白いと笑う、親しみやすく、相談しやすい先生です。
(取材・構成 渡辺 馨)


