一般に、物事が混沌としていてわけがわからない状況は「カオス」と表現されますが、「カオス(chaos)」は「初期値鋭敏依存性による長期予測の不可能性」を指す由緒ある学術用語でもあります。朝、少し寝坊していつも乗る電車より一本後の電車に乗ってしまい、この少しの遅れが次の乗り継ぎに波及して遅れが増幅され、最終的に目標とする時間より大幅に遅刻してしまった、という経験は誰にでもあると思います。この例に象徴されるように、初期値がほんの少し異なっただけでずっと後の状態に大きな変化が起きる場合は、未来の予測が困難であるため、「カオス」と呼ばれます。
一定の法則に従って時間変化する自然界の現象は微分方程式で記述されます。大抵の微分方程式は非線型であり、カオス的です。高校で学んだニュートン力学にカオスは登場しなかったと思いますが、三つの質点が万有引力で引き合う「三体問題」はカオスの例としてよく知られています。他にカオスの例としてよく挙げられるものは天気予報です。3日後の天気予報はそれなりに正確ですが、1ヶ月後の天気を正確に予測することは困難です。この理由は、天候を支配する気流の流れを記述する基礎方程式がカオスを示すためです。人類はカオスの概念を古くから持っていたようで、民謡などにもみられますが、カオスが科学の対象として明確に認識されはじめたのは20世紀後半に入ってからです。これには、コンピューターの発達が大きく関係しています。
カオスの本質の一部を捉えているモデルを紹介します。以下の図1のように、正方形を2つの部分に分解し、A、Bと名前をつけます。Aを横方向に2倍、縦方向に1/2倍してA’に写し、Bを横方向に2倍、縦方向に1/2倍してB’に写す変換を考えます。小麦粉の生地をこねてパンを作ったことはあるでしょうか?薄く引き延ばして、折り曲げ、また薄く引き伸ばして、折り曲げ、というプロセスを繰り返したことと思います。上の変換は、パン作りにおける小麦粉の生地の変化を数学的に表現しており、ベーカー変換(パイこね変換)と呼ばれます。正方形上の非常に近接したどんな二つの点も、変換を繰り返すことでやがて離れていきます。つまり、初期値の小さな誤差が次第に増幅され、後に大きな変化をもたらすのです。カオスの本質の一部は図形の「引き伸ばし」と「折り曲げ」という幾何学的性質にあり、パイ生地がよく混ざる理由は、「ベーカー変換がカオス的だから」なのです。
カオスの数学的研究が進むにつれて、ベーカー変換ではモデル化できないようなカオスが存在することもわかってきました。このようなカオスを研究するための新しいモデルを紹介します。以下の図2のように、正方形を4つの部分に分解し、A、B、C、Dと名前をつけます。Aを横方向に3倍、縦方向に1/2倍してA’に写し、Bを横方向に3倍、縦方向に1/2倍してB’に写し、Cを横方向に3倍、縦方向に2倍してC’に写し、Dを横方向に3倍、縦方向に2倍してD’に写す変換を考えます。C’とD’は正方形全体です。この変換では、領域A、Bから受ける影響とC、Dから受ける影響のバランスが鍵となります。図3はA、Bから受ける影響の方が大きい周期点をプロットしたものです。図4は、C、Dから受ける影響の方が大きい周期点をプロットしたものです。色の違いは周期の違いを表しています。周期を大きくしていくと、どちらのタイプの周期点も正方形を埋め尽くしますが、分布の仕方は異なっています。これらのことは最近、数学的に厳密に証明されました。二つの異なるタイプのカオスが切り分けられない形で共存しているため、この変換はヘテロカオス・ベーカー変換と呼ばれます。きわめて単純に見えるモデルですが、まだわかっていないことが多くあり、多くの研究者の興味を引きつけています。
図3、図4は齊木吉隆氏(一橋大学・教授)のご厚意による。
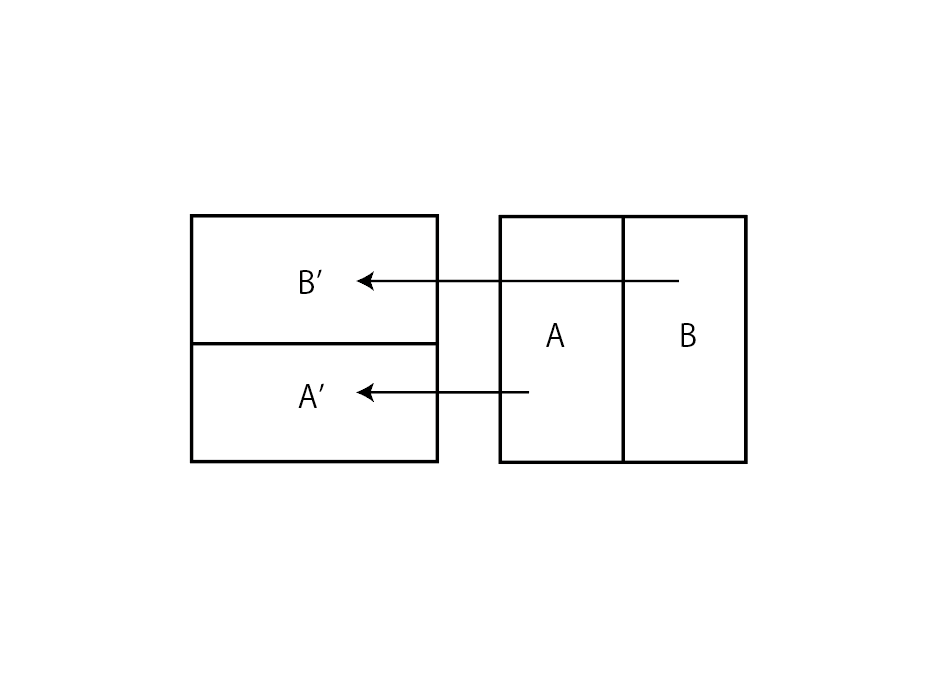
図1
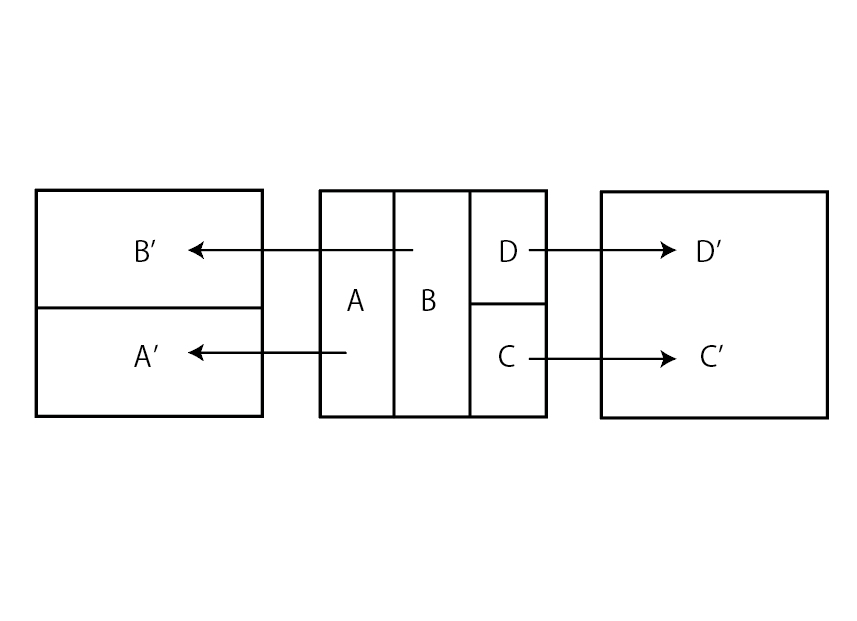
図2
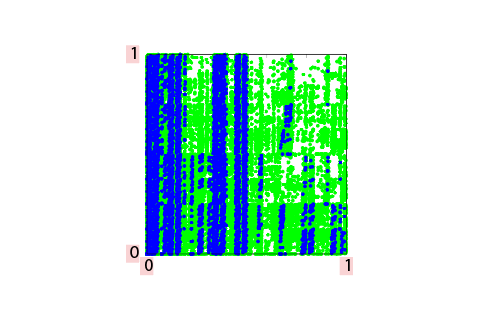
図3
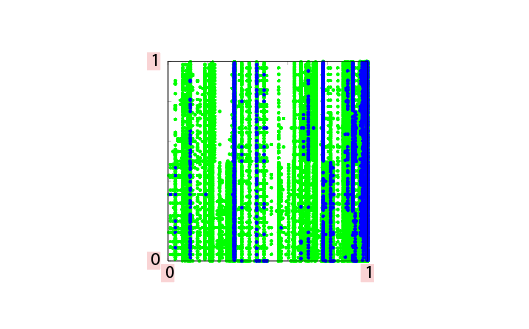
図4



