境界積分法(境界要素法と呼ばれることも多い)は偏微分方程式の境界値問題の数値解析法の一種である。この分野の研究者のバイブルである Linear Integral Equation (Rainer Kress, Springer) の Preface には "I fell in love with integral equations about twenty years ago when I was working on my thesis, and I am still attracted by their mathematical beauty." とあるが、Kress と同じく、私もこの方法に魅了され続けている者の一人である。面白いことに、(これは積分方程式に限らないが)美しい定式化に基づく数値解析は良い結果をもたらす場合が多い。そのような例の一つを我々の最近の研究成果(arXiv:2312.12787)をもとに紹介する。トランスミッション問題と呼ばれるある種の波動散乱問題に対して、境界積分方程式を素朴に立式すると悪条件となる(=これを離散化して得られる代数方程式の条件数が大きくなり、したがって求解に多くの計算時間を要する)ことが知られていた。我々は積分方程式を「適切に並び替えた上で一部を定数倍する」という単純な操作により、積分作用素(の二乗)から超特異作用素を全て消去できることを発見した。さらにはその固有値の集積点はただ一つであるという美しい性質を持つことも同時に明らかとなった。このようにして立式した積分方程式に基づく数値計算は従来法による計算と比して数倍から数十倍程度効率的であった。
また、境界値問題を解くばかりでなく、例えば物体の幾何学的特徴量を抽出する目的にも境界積分を使用することができる(図1)。CAD や 3D printing の分野では物体形状は境界の情報のみが(例えば STLとして)与えられるのが一般的であることから、(研究途上ではあるものの)工学の様々な分野で使いやすい方法論を構築できるのではないかと考えている。
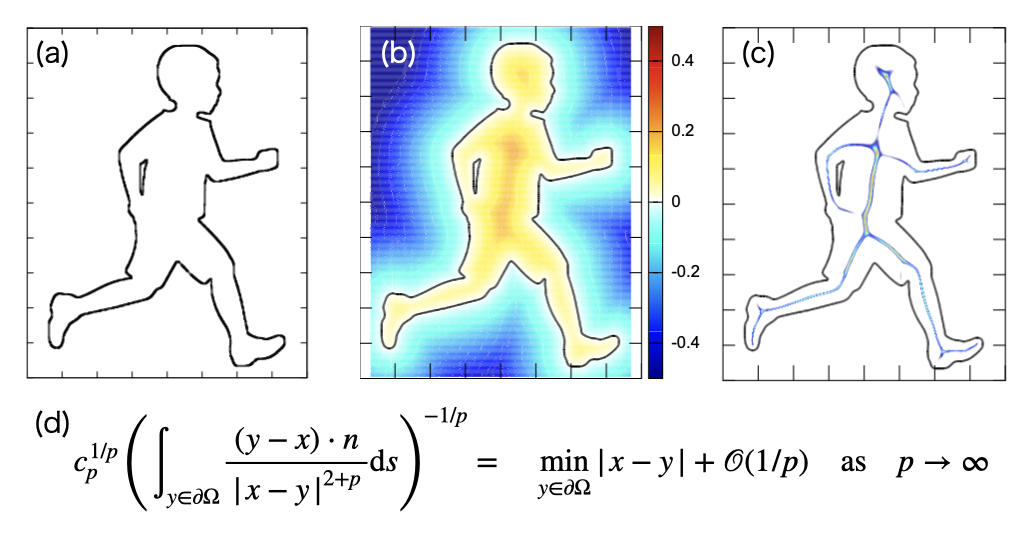
図1: (a) 与えられた物体の幾何学的特徴量として (b) 符号付距離関数、(c) スケルトンを抽出した例。(d) に使用した境界積分(一般化二重層ポテンシャル [2])を併せて示す。ここに、cp は定数、n は境界 ∂Ω における領域 Ω の外向き単位法線である。
Kupraze の時代から脈々と続く境界積分法研究を次世代へと紡ぐとともに、その他の要素技術(例えば数理最適設計)との統合を担う(自分自身を含む)若い世代の活躍を期待し、私からの「学問のすゝめ」とする。
[1] H. Isakari, 計算数理工学論文集, 2023.
[2] A. Belyaev et al, Computer-Aided Design, 2013.



