コイン投げをして表ならば右に裏ならば左に動くと、その動きはランダムウォークという最も典型的な確率過程になります。表と裏が出る割合によって、ランダムウォークの時間を大きくしたときの振る舞いが違います。例えば、表が出る割合の方が大きければ、最初の場所に戻ることなく無限遠点に行ってしまうという確率が正になります。ランダムウォークを一般化することによって様々な確率モデルが作られています。ここでは、その一つとして感染モデル(Epidemic model)といわれているものを紹介しましょう。
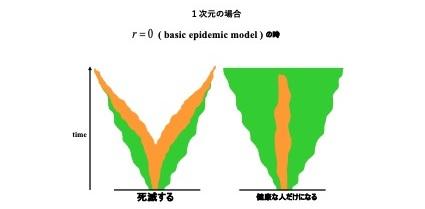
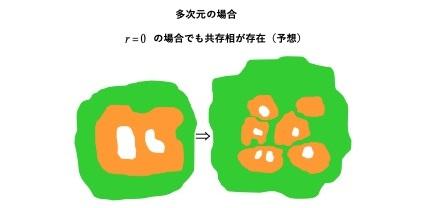
最初、健康な人と病気の人が少なくともそれぞれ1人ずつはいるとします。無人のところでは、隣の健康な人数の \(\lambda_{1}\) 倍の割合で健康な人が生まれます。健康な人は、隣の状態に関係なく割合 \(\delta_{1}\) で死亡し、隣の病気の人数の \(\lambda_{2}\) 倍の割合で病気になります。病気の人は、隣の状態に関係なく割合 \(\delta_{2}\)(>\(\delta_{1}\))で死亡し、割合 \(\gamma\)(≧0)で治癒して健康になります。このモデルでは、母数 \(\lambda_{1}\)、\(\lambda_{2}\)、\(\delta_{1}\)、\(\delta_{2}\)、\(\gamma_{1}\) の関係によって、時間を大きくしたときの振る舞いが異なります。さらに人が存在する空間の次元にも大きく影響します。2次元以上の場合は、回復率 \(\gamma_{1}\) が正であれば、母数を適当に与えると健康な人と病気の人が永久に共存する確率が正であることがわかります。割合 \(\gamma\) が零のとき、つまり治癒できない場合は、1次元の場合には、最終的な状態はすべての人が健康になるか、すべての人が死亡して無人になるかになります。つまり、健康な人と病気の人が共存することがないのです。2次元以上の場合は、まだ未解決ですが、健康な人と病気の人が共存することがあると予想されています。これは、病気の人のクラスター数が増えていき、病人の総数に比べて健康な人と病人の間(接触)の数が大きい共存が起こりえるからです。
実際の病気の感染に対応させて考えてみると、空間が1次元的であるというのは、接触する人数が少なく、すべての人が自宅で籠もっていることに、また高次元的というのは、密集した場所で多数の人と接触することに対応しています。このモデルでは、各人が移動しないで、隣の人数が固定されていますが、例えばランダムウォークで移動するようなモデルであれば、共存がさらに容易になります。クラスターについても、あまり複雑な形をしていない大きなクラスターが消滅しやすいのは、集団免疫をもつ(このモデルでは死亡になりますが)と感染が終息するということに関連しています。
最初、健康な人と病気の人が少なくともそれぞれ1人ずつはいるとします。無人のところでは、隣の健康な人数の \(\lambda_{1}\) 倍の割合で健康な人が生まれます。健康な人は、隣の状態に関係なく割合 \(\delta_{1}\) で死亡し、隣の病気の人数の \(\lambda_{2}\) 倍の割合で病気になります。病気の人は、隣の状態に関係なく割合 \(\delta_{2}\)(>\(\delta_{1}\))で死亡し、割合 \(\gamma\)(≧0)で治癒して健康になります。このモデルでは、母数 \(\lambda_{1}\)、\(\lambda_{2}\)、\(\delta_{1}\)、\(\delta_{2}\)、\(\gamma_{1}\) の関係によって、時間を大きくしたときの振る舞いが異なります。さらに人が存在する空間の次元にも大きく影響します。2次元以上の場合は、回復率 \(\gamma_{1}\) が正であれば、母数を適当に与えると健康な人と病気の人が永久に共存する確率が正であることがわかります。割合 \(\gamma\) が零のとき、つまり治癒できない場合は、1次元の場合には、最終的な状態はすべての人が健康になるか、すべての人が死亡して無人になるかになります。つまり、健康な人と病気の人が共存することがないのです。2次元以上の場合は、まだ未解決ですが、健康な人と病気の人が共存することがあると予想されています。これは、病気の人のクラスター数が増えていき、病人の総数に比べて健康な人と病人の間(接触)の数が大きい共存が起こりえるからです。
実際の病気の感染に対応させて考えてみると、空間が1次元的であるというのは、接触する人数が少なく、すべての人が自宅で籠もっていることに、また高次元的というのは、密集した場所で多数の人と接触することに対応しています。このモデルでは、各人が移動しないで、隣の人数が固定されていますが、例えばランダムウォークで移動するようなモデルであれば、共存がさらに容易になります。クラスターについても、あまり複雑な形をしていない大きなクラスターが消滅しやすいのは、集団免疫をもつ(このモデルでは死亡になりますが)と感染が終息するということに関連しています。