数学オリンピック予選で出会った恩師に導かれ、純粋数学の道へ
数学オリンピックの予選で知り合った友人に誘われて、ともに勉学に励み、数学者の道を目指すことになったという勝良さん。
その後、師事した恩師や異分野の共同研究者との出会い、国内外での数々の経験、そして家族が、研究者としての勝良さんのいまを支えている。
勝良 健史 / Takeshi Katsura
京都府出身。専門は作用素環論の中のC*-環論。特に力学系や集合論などと関連するC*-環の研究を行なっている。2003年、東京大学大学院数理科学研究科博士課程修了、博士(数理科学)。北海道大学、東京大学、トロント大学でのポスドクを経て、2008年4月より慶應義塾大学理工学部数理科学科専任講師。2012年4月より現職。
研究紹介
今回登場するのは、
純粋数学の一分野である C* 環論の研究を手がける勝良健史准教授です。
数学への根源的なモチベーションは「美しさ」にあり
純粋数学を追究することの魅力とは?
数ある学問の中でも、数学ほど文明社会の礎として欠かせないものでありながら、その幅広さと奥深さゆえに、一般に理解されにくい学問はないかもしれない。なかでも純粋数学と呼ばれる分野は、実学の対極にあって、専門家以外には見えにくい世界だ。その純粋数学の魅力や取り組み方、自身の研究分野である C* 環論の一端について勝良健史さんに聞いた。
問題を解くだけではない純粋数学の研究
ときに、「この数百年、未解決だった数学の難問がついに解けた!」などとニュースを賑わせることがある。しかし、その難問がいかにして解かれたかを理解するのは、専門家でも難しいとされ、証明が正しいことを精査するには何年もかかることがあるという。一般にはなかなか理解しにくい純粋数学の世界だが、数学者はどのようにして問題を解いているのだろうか。
「もちろん問題を解くことは純粋数学研究の主流ですが、研究をしていく上で価値のある問題を解くという経験はなかなかできません。まだ人類が誰も解いていない問題は、解く価値がないか、それとも解くのが不可能に近い難しい問題かのどちらかであることが多いですからね。また、解くのが難しいからといって価値があるとは限りません。解いた問題や得た結果の価値は、とても長い年月をかけて多くの科学者によって精査されます。抽象的な純粋数学の結果が、100 年後や 200 年後に思ってもみない具体的な形で応用されるなんていうこともあります。だからこそ、純粋数学の研究者は他人の意見には影響されず、それでいて他人に共感されるような独自の価値観、美的感覚を持つべきだと私は思います」と勝良さんは力説する。
しかし、問題を解くということが困難なら、そもそも数学者たちは何をどのようにして研究を進めているのだろうか。
「純粋数学の研究では、問題を解く、答えを出すということよりも、不思議な現象を見出し、それを理解するという面の方が強いと私は思います。不思議な現象を見出し理解するためには、対象をよく調査し仮説を立てて、さまざまな実験を通して検証する必要があります。このようなアプローチは、理工学の他の分野と似ているのではないでしょうか。ただ、対象が数学的対象と呼ばれる抽象的なものであり、実験にコンピュータを使うことが多いとはいえ、思考実験が中心であるという点は純粋数学の特徴だと思います。
また、どんなに成り立っていそうなことでも、きちんと証明ができなければ結果とは言えないのも数学の別の特徴です。証明すべき現象を発見したのに、それを証明できないときは、予想として発表することも数学の重要な研究成果の 1 つになります。私も世界の数学研究を引っ張るような予想を発表してみたいですね。もちろん、それを証明できればもっといいのですが」。
集合が持つ構造に着目し、関係性を調べる
目には見えず手で触ることもできない数学的対象をいったいどのようにして調べるのか。キーワードとなるのは集合と構造だと勝良さんは言う。
「最もなじみ深い数学的対象といえば、自然数や整数、実数などの数でしょう。そして、数を調べるときに、1 つひとつの数を個別に扱うのではなく、ある性質を満たす数を全部集めたものを調べるという考え方があります。このように、ある数学的対象を集めたものを数学では『集合』と呼びます。例えば、自然数全部の集合は N と表され、無限集合になっています。また、実数全部の集合 R はよく数直線として表現されます。
このような数の集合には、自然とさまざまな『構造』が入っています。例えば、実数全部の集合 R の数直線としての表現は、2 つの実数の大小という『関係』や 2 つの実数の間の『距離』などの構造を表現したものと言えます。これらの構造以外にも、数の集合は足し算や掛け算などの『演算』と呼ばれる構造を持ちます」(勝良さん)。
このようなさまざまな種類の構造を、写像(※1)などの集合論の言葉で記述することで、構造そのものを調べることが可能になるのだという。
「ある構造に注目するごとに、その構造を持つ集合というのが数学における研究対象になります。例えば、距離という構造から幾何学の分野の対象である距離空間や位相空間(※2)という概念に行き着くし、足し算や掛け算などの演算という構造から代数学という分野の対象である群や環、体(※3)といった概念に行き着きます。現代の純粋数学の研究では、そういった数学的対象の例を探したり、そのような対象が共通に持つ性質や異なる対象の間の関係を調べたりすることが、よく行われているのです」(勝良さん)。
なかでも、勝良さんがとくに興味を持って研究に取り組んできたのが、異なる構造(環と距離空間など)の間の関係や、複数の構造(群と位相空間など)を同時に備える対象だという。
「私がこれまで研究してきた C* 環(※4)と呼ばれる対象は、先ほど述べた距離空間や環という構造の他に線形空間や「*」(スター)と呼ばれる構造が定まっていて、これらの構造間に定義されるさまざまな条件(※5)を満たしているもののことです。C* 環は、力学系(※6)や位相空間、体など他の数学的対象と不思議な関わりを持ちながら今でもさかんに研究されている対象です。私はこの C* 環をとても可愛らしいやつだと思っているのですが、そのイメージを短い文章でわかりやすく伝えることはできません。わかりやすい説明には、不正確さや嘘が混じっているものですからね」と、勝良さんは笑う。
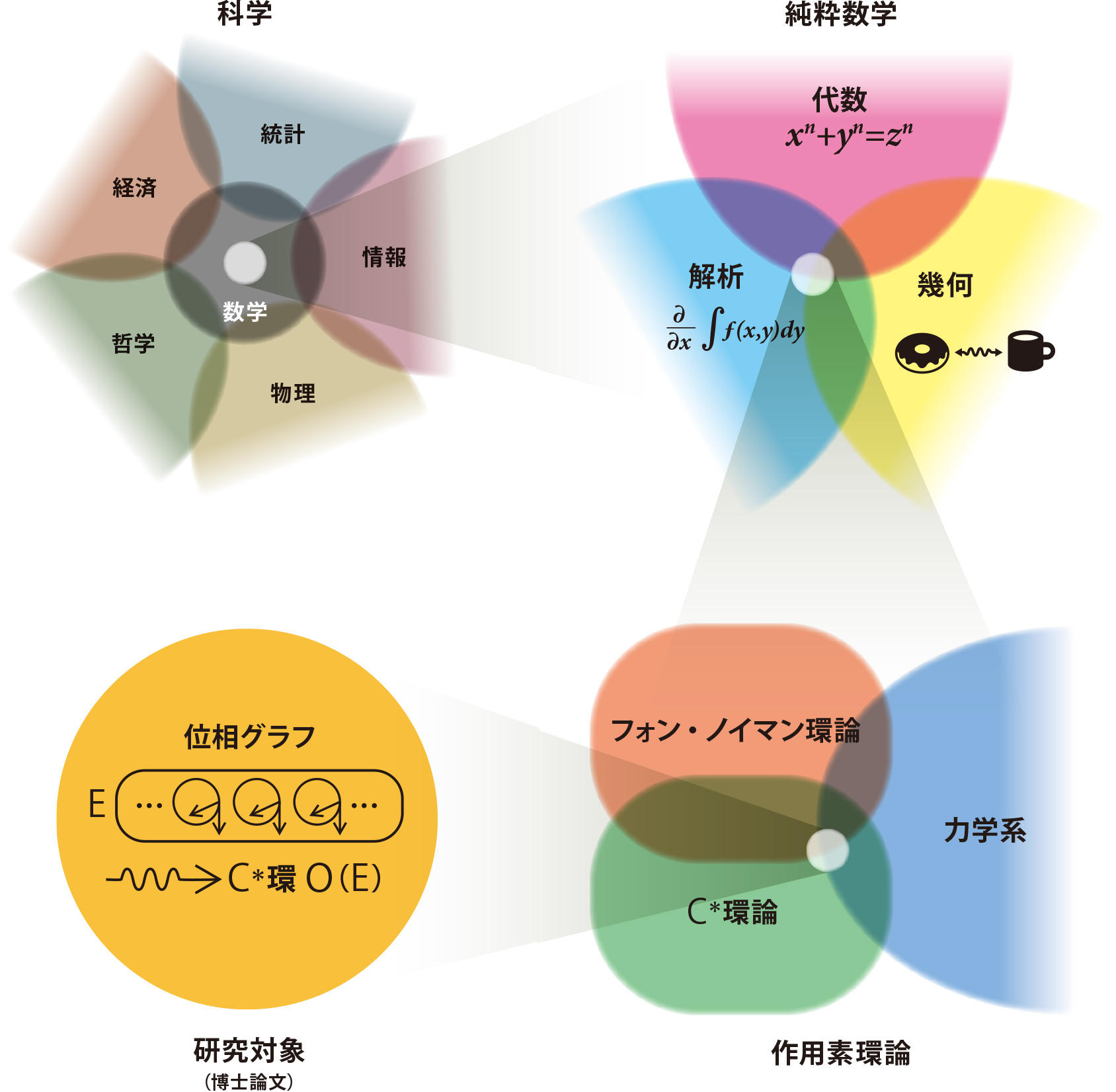
図 勝良さんの博士論文の位置づけと関連領域
勝良さんは、さまざまな分野と関わりのある数学という分野の中でも、「純粋数学」と呼ばれる他の分野とは直接関係のない研究分野に関心を持ちながら、純粋数学の中ではさまざまな分野と関連するところに興味を持っている。博士論文では、作用素環論の中の「C* 環論」と物理学に関連する「力学系」の交わる部分で、新しい視点を提供したが、最近は、哲学に近いといわれる集合論寄りの数学に興味を持っている。
境界領域に挑み、新たな数学を切り拓きたい
勝良さんは、抽象化された数学世界を研究することに、どのような意義を見出しているのだろうか。
「一番のモチベーションは、そこに美しさを感じる、ということです。問題に向き合うなかで、ときに本当に美しいと思える真理を見出すことがあります。19 世紀に、複素解析学(※7)と呼ばれるとても美しい分野が数学者によって発見されました。この複素解析学が 20 世紀になって、フォン・ノイマンらによる量子力学の数学を用いた記述においてとても重要な役割を果たし、そしてその成果は半導体を通して現在の社会を支えています。このように、本当に美しい数学というのは、後世に思ってもみない形で応用されることが少なくありません。私も後世に残る成果を残したいですね」と、勝良さんは意気込む。
今後は、C* 環論だけでなく、力学系、整数論、集合論など、さまざまな分野の境界領域に研究対象を広げ、未解明な数学の新たな領域を切り拓いていきたいと展望を語った。
インタビュー
勝良健史准教授に聞く
算数は得意な方だったが、計算は苦手
どんな幼少期を過ごされたのですか?
生まれは京都府向日(むこう)市で、いわゆるベッドタウンで育ちました。父がボードゲームやパズルが好きな人で、家にオセロやジグソーパズル、バックギャモン、ルービックキューブなどさまざまな遊び道具があって、幼い頃からよくそれらのゲームで遊んでいました。家族で過ごすときも、ボードゲームをよくやっていましたね。
もっとも、小学生くらいの頃は、屋外で遊ぶのも好きで、中高時代はサッカー部にも所属していました。そのほかの遊びといえばもっぱら麻雀をやっていました(笑)。
やはり幼い頃から算数が得意だったのですか?
算数は得意なほうでしたが、計算は決して得意ではありませんでした。今でも計算は苦手です。好きだったのは、知能テストに出てくるようなパズルや図形の問題です。
中学受験のときに挫折を味わいました。洛星中学・高校入学を目指して勉強していたのですが、入試のときに算数で1問だけどうしても解けない問題があって、その問題に固執するあまり、ほかの問題を見直さなかったら、たくさん計算ミスをしていたのです。その前に東大寺学園に合格していて、受かったのが友達の中では私だけだったので、少し気が緩んでいたこともあるのでしょう。結局、友人たちは洛星へ、私だけが東大寺学園に行くことになりました。東大寺学園は自由な校風でのびのびと勉強ができたこともあり、結果としてはよかったのですが、以来、数学の問題を解く際には、別の方法を使ったりして、3〜4回答え合わせをするのが習慣になりました。中学受験での挫折がいい教訓になっています(笑)。
いつから数学を研究しようと思われるようになったのですか?

純粋数学の面白さに触れたのは、高校2年の終わりに、数学オリンピックの日本代表候補20名に選ばれたのがきっかけです。選抜合宿に参加すると、自分よりも数学の知識に通じていて、すぐに本質を見抜いてしまうような非常に優秀な人たちがたくさんいて驚きました。それまで、自分より数学ができる学生に出会ったことがなかったので、たいへん刺激を受けました。 残念ながら代表の6名には選ばれなかったのですが、高校3年の夏に代表候補者などが集う合宿に参加することになり、そこで出会った同級生が私の人生を変えることになります。彼らから、一緒に東京大学へ進学して、数学を勉強しようと誘われたのです。そこで、地元に近い京都大学ではなく、東大への進学を決めました。東大理科1類に進学し、上京して1人暮らしを始めることになりました。 入学してからは授業にはあまり出ないで、その友人たちとテキストを決めて、週に1度集まって輪講していました。その頃は、とにかく数学の知識を吸収することに必死で、かなりの時間を費やしていましたね。
飛び級で学部3年から修士課程に進学
では、大学時代は数学に没頭していたのですか?

数学の勉強以外にも、その友人の誘いで塾の講師のアルバイトもしていました。中高生に大学の数学を教えるという塾で、カリキュラムやテキストも自分たちでつくるなど、アルバイトでありながら主体的に関わっていました。そのときの経験が、人に教えるという現在の仕事につながっていると思います。 それから、さまざまな大学の学生が集まるインカレの山登りサークルにも参加していました。3泊4日といった日程で、南アルプスなど3,000m級の山にテントを持って登ったりしました。慶應大学の学生も多く、管理工学科の田中健一先生とはこのサークルで出会って以来の友人です。田中先生もそうですが、私も妻とはこのサークルで知り合ったんですよ。
学部のときに飛び級されたのですね?
ええ、これもその友人たちの誘いで、3年生しか受けられない飛び級試験を受けて、ともに学部3年で中退し、修士課程へ進学しました。友人2人は整数論を選びましたが、私は作用素環論を専門とされている河東泰之先生の研究室に入りました。
河東研究室のセミナーでは、ノートを見ないで話をすることを要求されました。このスタイルは、私の研究室でも踏襲しています。最初は大変でしたが、これは暗記を強要するものでは決してなくて、きちんと問題を理解して、自分の頭で再構築する力を養うための方法論です。数学に限らず、こうした訓練をしておくことは、社会へ出てからも役立つと思います。
修士課程2年のときには、カリフォルニア大学バークレー校の数学研究所MSRIに1年弱ほど留学の経験もしました。
その後、博士課程を2年で修了して結婚し、東大大学院数理科学研究科で学術振興会の特別研究員(PD)として研究を続けました。この時期に、オレゴンでの長期滞在も経験することができました。それから、学術振興会の特別研究員(SPD)として、北海道大学大学院理学研究院で3年間、のびのびと研究生活を過ごしました。3年間世界を飛び回っていたのですが,この間に培った人間関係が、いまの自分の研究を支える基盤になっています。
もう1つ、北大時代に得たことといえば、札幌の喫茶店で漫画『ヒカルの碁』を読んで、囲碁に目覚めたこと。現在は、囲碁三段です。
狭い門をくぐって慶應義塾大学理工学部の専任講師に
数学者はいまでこそ企業から引っ張りだこですが、一方で、数学研究者の就職は難しいとも聞きますね。
数学研究者というのは狭い門なので、研究の実力の他にもタイミングや運が必要なのだと思います。私が博士課程を修了したころは、研究者を目指す若い人が増えていたのに職の数は減っている時期だったので、椅子を勝ち取るのは熾烈な戦いでした。結局、北大のあとは半年間東大のポスドクをしたのちにトロント大学のポスドクになりました。トロント大学に向かう直前に慶應大学から採用の内定を得たので、トロントでの滞在を予定より短く半年で切り上げ、2008年4月から慶應義塾大学理工学部数理科学科の専任講師として着任しました。とても良い大学に就職できたおかげで、5年間のポスドク時代も無駄ではなかったと感じます。慶應大学に着任してからは、デンマーク大学にも滞在する機会を得ました。
慶應大学理工学部の良さは、先生と生徒の距離が近く、まさに「半学半教」を実践しているところですね。真剣に議論したり、お酒を酌み交わしたり、アットホームな雰囲気の中で過ごすことができ、とても気に入っています。また、私が知っている国内外の数学系の学科とは異なり、慶應大学の数理科学科は純粋に数学の理論を究めるだけでなく、数学の応用にも力を入れています。学生も卒業後は研究者になる人は少数で、教員になったり企業に就職するなどさまざまな方面へ進む。統計や計算機科学の研究室など、幅広い学科の教員同士の交流も盛んで、私自身、視野が広がったと感じています。
先生ご自身も共同研究をなさるのでしょうか?

ええ。最初は1人で研究していたのですが、トロントにいたときに、集合論の研究者が私の論文を読んで、ある問題に一緒に取り組まないかと研究室に訪ねてきたことがあるのです。その問題は30〜40年ほど解かれていなかった難問でしたが、一緒に研究することで解決できました。以来、私自身も積極的に他の研究者に声をかけるようにしています。
どういうときにひらめくのですか?
問題を解く際には、いくつかの例や現象の共通点を見出して、文章化するのが肝です。そうやってずっと考えていると、リラックスした瞬間にふとひらめくことがある。シャワーを浴びていたり、歩いていたり、いろいろです。ひらめいたときは、嬉しくて、思わず共同研究者に電話をしたこともありました。
だからこそ、一緒にいてリラックスできる家族の存在はとても大切だと感じています。私の良き理解者である妻と、小学3年の長男、年長の次男の4人家族です。長男は囲碁の腕前はすでに私と同じ三段で、負かされることも(笑)。神奈川県代表にも選ばれたんですよ。次男も私に似て、ボードゲーム好きで、だんだん強くなってきており、将来が楽しみです。
どうもありがとうございました。
◎ちょっと一言◎
学生さんから
●勝良研究室に入ったきっかけは、先生の授業が圧倒的に面白く、難しい問題もイメージしやすかったから。確かに、セミナーのときにノートを見てはいけないというのは大変ですが、物事を自分で理解して、筋道を立てて人前で話すうえで、とてもいい訓練になっています。
(取材・構成 田井中麻都佳)


