人がやっていないマイナーなことを根気よく続けるのが面白い
これまで、珠算、卓球、競技ダンスなど、いずれも少しマイナーだが、
奥深い世界が広がる趣味やスポーツを、根気よく続けてきたという湯川さん。
その姿勢は、流行の研究に飛びつくことなく、
理論研究を究める研究者としての湯川さんの姿勢と重なる。
その陰には、家族の支えや、友人、恩師とのかけがえのない出会いがあった。
湯川 正裕 / Masahiro Yukawa
専門は凸解析・不動点近似に基づく信号処理工学。数理科学の知見を活かして信号処理分野に新しい地平を拓くことを目標に研究している。東京工業大学工学部電気電子工学科卒業(2002年)。同大学院博士課程修了(2006年)。英国ヨーク大学博士研究員(日本学術振興会特別研究員PD)、理化学研究所基礎科学特別研究員、ミュンヘン工科大学客員研究員、新潟大学工学部准教授などを経て、2015年4月より現職。
研究紹介
今回登場するのは、
信号から自在に情報を抽出する万能な適応フィルタを手がける湯川正裕准教授です。
信号から役立つ情報を取り出す適応フィルタとは
複雑な事象を読み解くための「万能フィルタ」をつくりたい
画像、音、電波、脳波、さらには株価の変動など、世の中にはさまざまな信号(情報)が存在する。その信号を数値化することによって欲しい情報だけを抽出し、その事象の特徴を見出したり、予測を立てたりするのが信号処理の役割だ。湯川正裕さんは、森羅万象から得た複雑な信号を、数理的なアプローチによって扱いやすい状態にし、必要な情報を抽出する際に役立つ数理体系の構築を手掛けている。
信号処理は電子産業の基盤
「仮に、この世から信号処理がなくなったとしたら、テレビも携帯電話もデジタルカメラもなく、飛行機も飛ばない世界になるでしょう。医療機器のMRI も信号処理の産物ですし、最近話題のドローンやアンドロイドロボット、ビッグデータ解析なども信号処理がなければ実現できません。つまり、信号処理というのは現代人にとってみれば、空気のように不可欠な存在なんですね」と、湯川さんは語る。
例えば、携帯電話の音声であればマイクで、デジタルカメラで撮影した画像なら撮像素子で、それぞれ電気信号に変換される。こうした電気信号を数値の列に置き換えれば、すべて数学的な処理が可能になり、いわゆる信号処理の対象となるのだ。
「実際に私が手掛けてきたのは、音響と通信の適応信号処理です。一例として、エコーキャンセラがあります。これは、テレビ会議や携帯電話の通話などで、自分がしゃべった声が相手のマイクを通じて遅れて返ってくると耳障りなため、返ってきた音声だけをカットするというもの。信号処理によって、返ってきた自分の音声は不要なので引き算して、相手の音声のみを届けるのです。通信の場合も同様に、同時に基地局に届く複数の通信データを、適応信号処理でユーザーごとに切り分けて届けます。その信号処理に欠かせないのが、必要な情報だけを取り出す『適応フィルタ』です」。
データから関数を推定するのが適応フィルタの役割
適応フィルタは、まさにコーヒーのフィルタのように、数学的なフィルタを通して、必要な情報だけを取り出す役割を担う。
「音声であれば、観測された音声(y)から欲しい音声(x)を取り出せる関数(f)を推定するのがフィルタの役割。つまり、yからxを推定したいわけですから、関数fを求めればいいのです」と湯川さんは説明する。
ただし、「適応」とあるように、人が動くなどして時々刻々と変化する状況に応じて、柔軟にフィルタの係数を変化させなければならない。つまり、計算量を抑えつつ、リアルタイムに欲しい情報にできるだけ近づけた関数を表現できるかどうかが、適応フィルタの良し悪しを左右することになる。
ところが、実際の事象は非常に複雑で、数学的に扱うのが難しい非線形性を持つ場合がほとんどだ。非線形とは線形ではない、簡単に言えば、入出力が比例関係にないこと。非線形なデータを扱おうとすると、とたんに計算量が増えて、素早く情報を取り出すことが難しくなる。
「非線形なデータに対するアプローチとしては、ヴォルテラフィルタやニューラルネットワークなどがありますが、前者は計算量が膨大になる、後者は局所最小解に陥るという欠点があります。そこで、私が採用したのが、カーネル法を応用した『再生核(カーネル)適応フィルタ』という手法です」。
カーネル法とは、データを高次元の特徴空間に写像する(例えば、2次元データを3次元へ写す)ことで、データ群を別の扱いやすいデータ群へと変換する手法のことをいう。これは顔認証などのパターン認識やビッグデータ解析などに広く使われている手法で、従来は、集めた情報をすべてまとめて一度に処理するバッチ処理に採用されてきた。最近では、時々刻々と新しいデータが取得されるオンライン処理でも活用されている。
「再生核を説明するのは専門的で難しいので割愛しますが、このカーネル法が優れているのは、関数の値を『内積』で表現できるところにあります。内積の簡単な例は、2つのベクトルの要素を順番に掛け合わせ、それらをすべて足し合わせたもの。これにより、2つのベクトルの相関が表現できるようになります。そして、内積で表現できれば、線形モデルの知見を存分に用いることができるようになるのです」と湯川さんは強調する。
つまり、扱うのが難しい非線形のデータを、計算しやすい線形の理論によって取り扱える点が、この手法の最大の特長と言える。
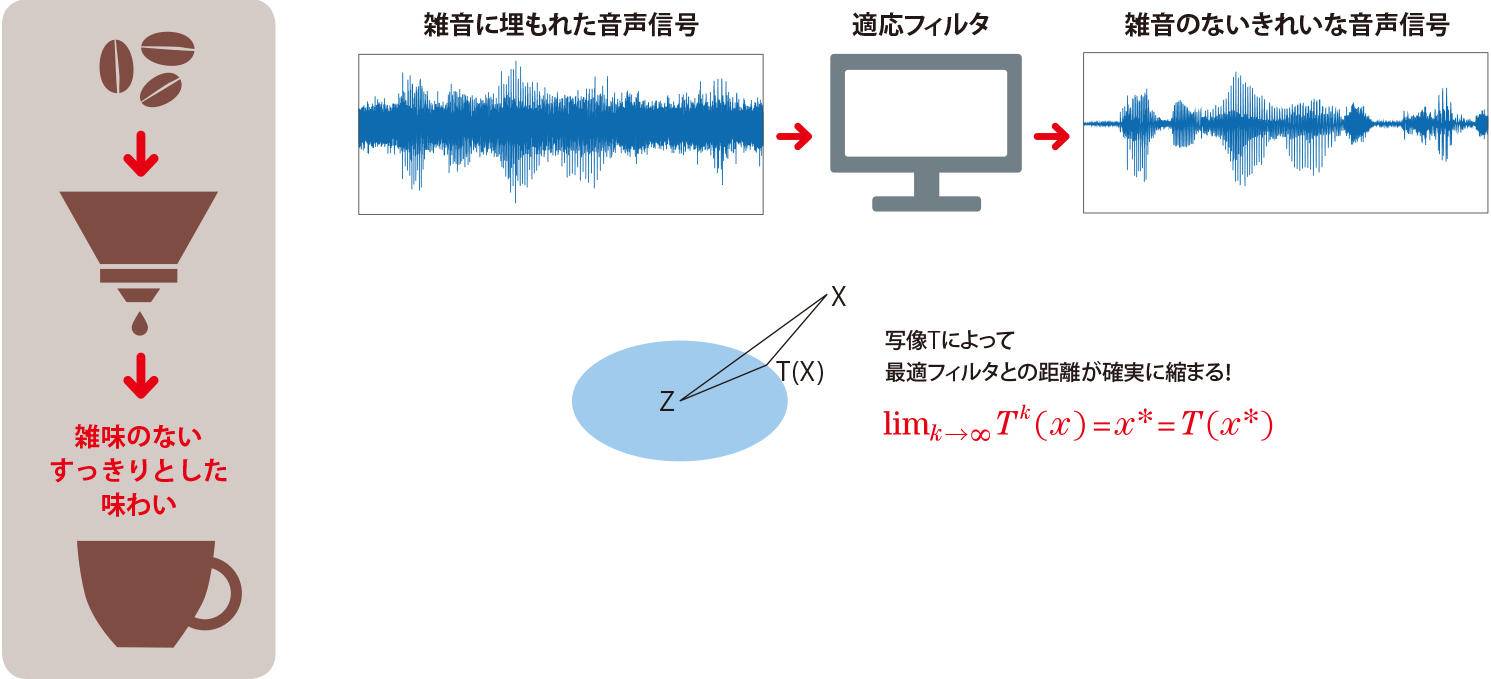
図 1 適応フィルタの応用例と基本原理
雑味を取り除くコーヒーフィルタのように、雑音を除去してクリアな音声信号を取り出すために用いることができる。フィルタ係数を更新するための基本的なアルゴリズムは、距離射影と呼ばれる非拡大写像の一種に基づいている。写像 T が「不動点を持つ非拡大写像」と「恒等写像」の加重平均であるとき、T を繰り返し作用させることで不動点 x*に収束することが知られている(Mann の不動点定理)。
リアルタイムに欲しい情報を取り出す
この再生核適応フィルタをベースに、凸最適化と呼ばれる分野の最新の知見を駆使して湯川さんが開発したのが、「多核適応フィルタ」である。
「イメージとしては、再生核の一種であるガウス核と呼ばれる山形の曲線の足し合わせで関数の波形を近似するという手法です。幅が広く低い山や幅が狭く高い山など、いくつものガウス核をあらかじめ用意しておいて、その高さを決める係数を並べて行列にします。そして、なるべく少ない山の足し合わせで関数を推定していくのです。
その際、推定したい関数にフィットする山を自動的に特定し、それ以外の大多数の山の係数をゼロにする仕掛けが 1 つ の ポ イ ン ト で す。 ゼ ロ を た くさん含む行列のことをスパース行列(sparse はまばらという意味)と言いますが、情報をうまくまとめること(スパース化)で、最適なモデルの選択を可能にするのです」。
これにより、非線形関数の形に合わせて、ガウス核の幅を適応的に自動調整することが可能になり、関数の形が時間の推移とともに変化しても自在に対応できるようになった。より少ない山の数で高精度な推定ができるという。
「この手法を使うと、例えば、太陽光発電において、過去の発電量のデータから、リアルタイムに未来の発電量を高精度に予測することが可能です」。
その湯川さんの研究の数理的基盤となっているのが、「非拡大写像の不動点理論」というものだ。
「不動点とは、写像 T を施しても動かない点、つまり Tx = x となる x のことを言います。また、2点間の距離が写像を施した後に拡大しないという性質を非拡大性と言います。自然科学から工学まで、様々な領域において、問題の解をある写像の不動点として表現できることがわかってきています。そして、その写像が非拡大性を持つとき、この非拡大写像を使って不動点、つまり問題の解を求めるアルゴリズムを容易に設計できるのです。多核適応フィルタでは、時間の推移とともに変化する未知の関数を、時々刻々と入手されるデータを用いて作られる写像の不動点として表現し、これを手がかりに未知の関数を推定していくわけです」。
将来的には、どんな複雑な事象にも対応できる究極の「万能フィルタ」をつくりたいという湯川さん。今年に入って複数の論文が IEEE(米国電気電子学会)のジャーナルに掲載されたり、信号処理のトップジャーナルのエディターに抜擢されたりと、国際的な評価も高まっている。分散型信号処理やビッグデータ解析、ディープラーニングといった流行の研究を横目に、その基盤となる数理体系の構築を目指して、日々研究を続けている。
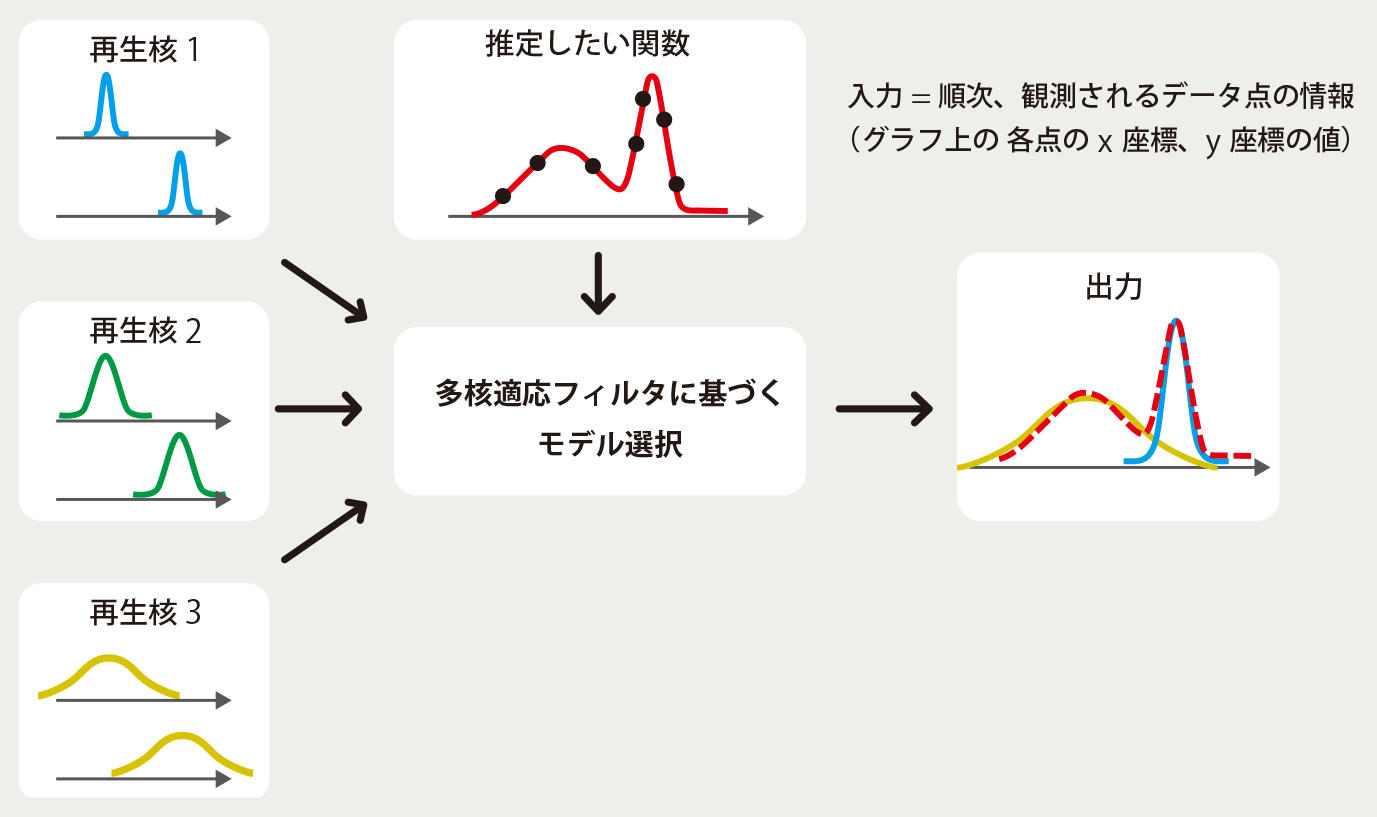
図 2 多核適応フィルタに基づくモデル選択の概念図
順次、観測されるデータ点の情報を用いて適応アルゴリズムで学習させることにより、推定したい関数の局所的な特徴を適切に表現できる数理モデル(再生核)を自動的に選択することが可能となる。適応アルゴリズムには、「スパース表現」と「非拡大写像の不動点理論」の知見が活きている。
インタビュー
湯川正裕准教授に聞く
幼少期から暗算や算数が得意で、
しだいに数学に興味をもつ
どんな幼少期を過ごされたのですか?
どうやらおしゃべりな子どもだったみたいで、保育園の先生に家で起きた出来事を、逐一、話していたようです。しかも、はきはきと、わかりやすく話していたようで……自分ではあまり覚えていないのですが、両親は「かなり恥ずかしい思いをした」と言っていました(笑)。
それから、いつも4つ上の姉の後をついて歩いては、一緒におままごとなどをしていて、「金魚のフン」と言われていましたね……(笑)。
出身は神奈川県南足柄市です。父も母も公務員で、父は小田原市役所、母は大蔵省印刷局に勤めていました。理数系の科目が得意だった両親の遺伝子を受け継いだのか、幼稚園の頃から暗算が得意だったと聞いています。ただその頃の記憶はあまりなくて、覚えているのは小学生の頃に、母の買い物について行って、金額を暗算していたことくらいでしょうか。
数学的な興味という意味では、なぞなぞとかクイズ、パズル、算数に関する本は好きでよく読んでいました。それ以外は、『ドラゴンボール』や『聖闘士星矢』など、流行の漫画を読むくらいで、読書はあまりしない子どもだったと思います(笑)。
小学校に入学すると珠算を習うようになり、先生の指導がよかったこともあって、中学2年まで続けました。珠算は初段、暗算は三段を持っています。競技会ではいつも上位に入賞していて、小学6年生の時には、読み上げ算で、神奈川県大会で優勝したこともあるんですよ。昔ほどではありませんが、今でも二桁くらいの足し算やかけ算は暗算で計算します。
算数や数学を友達に教えていたこともあります。今から思えば、友達に教えることで、自分の勉強にもなっていたのでしょうね。友達には感謝しています。
インドア派だったのですか?
いえ、家の周囲に田んぼが広がっていて、よく、田んぼや花畑など外で遊んでいました。小学校では休み時間の度に、校庭にダッシュしていって、クラスの皆とボール遊びをするような、活発な子どもでした。学校に行くのが好きで、朝、6時に登校しては、友達と一緒に持久走の練習をしていたこともあります。そのほかにも、クラブで野球をしたり、スイミングスクールで水泳をしたり、身体を動かすのは好きでしたね。中学では卓球部のキャプテンを務め、県大会にも出場しました。身体を動かす分、睡眠もよく取っていました(笑)。
一方で、ファミコンやゲームボーイに夢中になった時期もありました。飽きるまでやって、中学に入る頃には、本当にすっかり飽きてしまい、ゲーム遊びは卒業しました(笑)。
ご両親から「勉強をするように」と言われることはなかったのですか?

なかったですね。宿題など、最低限の勉強はしていたし、授業もしっかり聞いていたと思うので、勉強のことで叱られたりしたことはありませんでした。基本的にやりたいことを好きなだけやらせてもらえる環境で育ててもらったことに感謝しています。小学生の頃に、プラモデルをつくっていて、家の絨毯(じゅうたん)をボンドでベタベタに汚してしまったことがあるのですが、それでも怒られた記憶はありません。それくらい、寛容な親だったのでしょうね。
中学生になると姉の影響もあり、地元の小さな塾に行くようになりました。塾の先生の熱心な指導のおかげもあって、ますます数学の勉強が楽しくなりました。ただ、将来は研究者というよりも、公認会計士になろうかなと考えていました。
高校は学区外の県立厚木高校に進学し、小田急線に片道40分乗りながら数学の教科書を読むのが日課でした。これが、現在の研究者としての血肉になっているのかもしれません。
一方で、社会勉強と小遣い稼ぎを兼ねて、1年生の途中から2年生の終わりくらいまで、クラスの友達と一緒に、高校の近くの生協でアルバイトをしていました。お惣菜コーナーでバイトしていたこともあって、ピタっときれいにラップをかけるのが特技なんですよ。この特技で、妻にびっくりされたこともあります(笑)。
バイトで稼いだお金は、アコースティックギターを買うなど、音楽に使っていました。「スピッツ」とかJ-Popの弾き語りをしていましたが、人前で演奏するほどではありませんでした……(笑)。
高校3年生から受験を意識し始め、理系の大学を目指して、進学塾に通うようになりました。秋の文化祭ではクラスの仲間とダンスや出し物に熱中しましたが、その後のラストスパートでなんとか大学に合格したという感じです。
学部時代は競技ダンスとアルバイトに打ち込む
大学は東京工業大学第5類に進学されましたね。
友人のお父さんの薦めと、予備校のチューターの意見を参考に選びました。この頃には、将来は情報系や数学系の知識を使った仕事をしたいと漠然と考えるようになっていました。
ただ、低学年のうちはそれほど真剣に勉学に励んだわけではありませんでした。フーリエ変換やラプラス変換など、理論系の講義には興味を持って出ていましたが、まだ、何を勉強したらいいのか、あまりピンときていなかったのだと思います。そうしたことから、学部生の頃は、部活動とファストフード店でのアルバイトに精を出していました。ファストフード店でのバイトは、他大学の学生との交流の場であり、サークル活動のように楽しい時間を過ごしました。
それから、大学に入ってから始めたのが、競技ダンスです。きっかけはテレビ番組の影響でしたが、マイナーなことというか、皆がやっていないことをやってみたいという思いがあったんですね。競技ダンス部には各学年で男性は4人程度しかいませんでしたから、相当にマイナーですよね(笑)。そういう意味では、珠算や卓球に通じるところがあるかもしれません。研究はどうかというと、信号処理は世界的にみてすごくメジャーな分野なんです。でもその中で私は他の人が目をつけていないところに焦点を当てて研究しています。
競技ダンスではラテンが専門でしたが、結局、10年ほど続けました。実は留学先にイギリスを選んだのも、競技ダンスの影響という噂も(冗談)。もっとも、イギリスでは競技ダンスではなく、もう少し趣味的な社交ダンスに近い練習会に、毎週、顔を出していたのですが……。
意外ですね。女性と踊るのは照れませんでしたか?(笑)。

最初こそ照れましたが、すぐに慣れました。実は、結婚してから妻を誘って一緒に社交ダンスをしていたことがあるのですが、結局、数回で妻が音をあげて、辞めてしまったのです。私が厳しく指導するので嫌になったと言って……(笑)。そんなに厳しくしたつもりはないのですが、つい競技ダンスの名残で、姿勢や重心の移動などを細かく注意していたようです。何事もやり始めると集中してしまうのは、いいところでもあり、悪いところでもありますね。
研究の面白さにはまったのは大学4年になって、信号処理と通信理論の研究室に入ってからです。実は当初、コンピュータビジョンの研究室に入ろうとしていたのですが、その研究室が定員オーバーで、ジャンケンで決めるというので希望を変更したのです。今から思えば、理論系の研究室に進んで大正解でした。
修士課程になると、国際会議で発表したりするようになり、ますます研究にのめり込むようになりました。そして、研究の世界で生きていきたいと強く思うようになり、博士課程に進学しました。途中からは日本学術振興会の特別研究員に採用され,給料や研究費をもらいながら研究できるようになりました。
博士課程修了後は、念願だった基礎科学特別研究員として、理化学研究所への就職が決まっていましたが、幸い、半年早く修了できたことから、その間、イギリスのヨーク大学に留学しました。帰国後、2007年4月から理化学研究所に3年間ほど勤め、移動体通信や適応フィルタの研究に取り組みました。理研時代には、4カ月間ほどですが、ミュンヘン工科大学にも留学していたことがあります。
その後、新潟大学(2010年4月〜2013年3月)での勤務を経て、慶應義塾大学に移ったというわけです。
いい恩師との出会いに恵まれ順調に研究を進める
順調に研究を進めてこられたのですね。

そうですね。根気よく研究を続けてこられた背景には、節目ごとに、いい恩師に出会えたことが影響していると思います。珠算や塾の先生もそうでしたが、東工大の山田功先生、理化学研究所の甘利俊一先生にはたいへんお世話になりました。
その恩返しもあって、学生には熱心に指導しているつもりですが、もしかすると鬱陶(うっとう)しがられているかもしれません(笑)。一方で、子どもに対しては、自分が親にしてもらったように、勉強のことはうるさく言わないようにしています。
研究の息抜きは?
小さい頃から食べることが好きで、食事が一番の息抜きですね。それから、至福の時は、コーヒーを入れてスイーツを食べながら、ジャズやラテンなどの音楽を聴いている時。学生とランチに行くのが日課で、コーヒーブレイクをともにしたりもしています。
慶應義塾の良さは?
広報が充実していて、私のような若手教員の研究をエンカレッジしてくれるのは非常にありがたいですね。学生にとっても、低学年のうちから教員と直接かかわる機会が多く、教員との距離が近いのは、とても恵まれた環境だと思います。さまざまなサポート体制があって、早くから進路が意識できるのも、まさに慶應義塾ならではの良さでしょうね。
どうもありがとうございました。
◎ちょっと一言◎
学生さんから
●研究に対しては冷静な目を持ちつつも、目標に対しては情熱的で、「世界一の研究室を目指そう」と言うのが湯川先生の口癖。ランチミーティングやコーヒーを飲みながらのアイデア出しやディスカッションなど、つねに会話と笑いの絶えない楽しい研究室です。
(取材・構成 田井中麻都佳)


