Research Spotlights #06

古代ギリシャ時代以来、何人もの数学者達が「辺の長さと面積が全て有理数であるような三角形」を探求してきました。このような三角形を「有理三角形」と呼びます。周の長さや面積は私たちの身の回りにあるものを測量する際に欠かせない基本的な「幾何学」的対象であり、有理三角形を周の長さと (または) 面積で分類するという問題が考えられてきました。これまでに、 周の長さ同士が等しく、また面積同士も等しい有理三角形の組が無限に多く構成されています([Bremner]、[van Luijk]やその参考文献を参照)。本稿では、私達の研究で得られた有理三角形に関する新しい定理をご紹介します。それは以下の通りです。

『周の長さ同士が等しく、また面積同士も等しい有理直角三角形と有理二等辺三角形の組は相似を除いてたった1組しかない。』

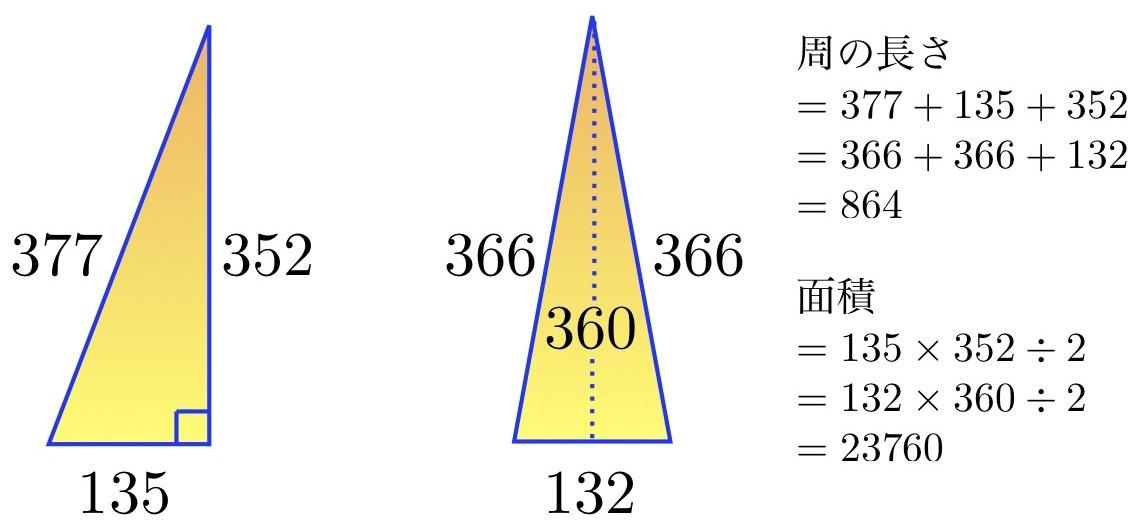
この定理の証明は特殊な種数2の代数曲線の有理点集合の決定に帰着されます。三角形の組の辺の長さはある正の有理数 x, u, k を用いて以下のように表されます。

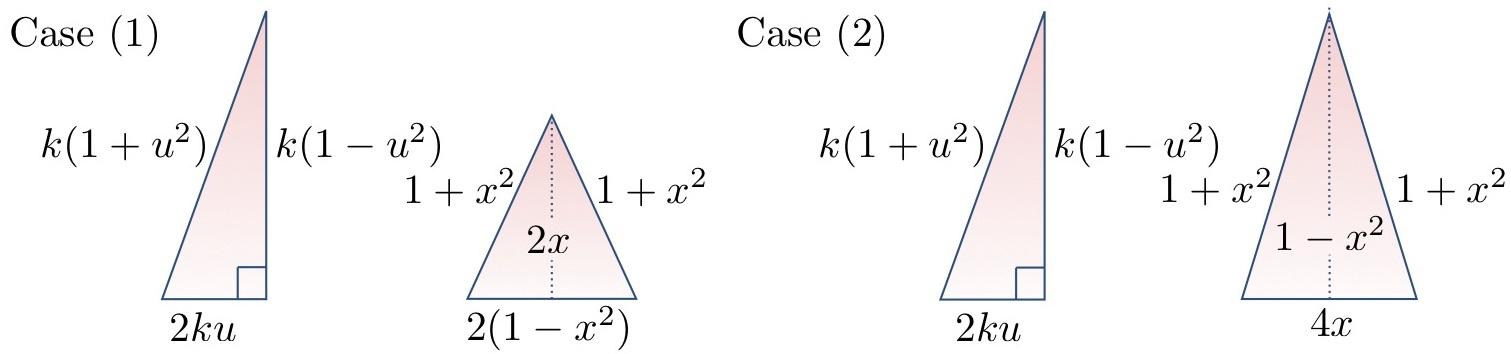
Case (1)では、y² =(x³ −x+6)² −32という代数曲線の有理点（方程式の有理数解）を全て決定します。一般には、種数2以上の代数曲線上には有理点が有限個しかないことが知られていますが、個々の代数曲線の有理点集合を完全に決定するためにはさらに高度な技術が必要になります。そこで、本研究では、p進Abel積分論に基づいたChabauty-Coleman法と呼ばれる解析的な手法(cf. [Coleman])を用いることで、上記の代数曲線上には有理点が10個しかないことを証明しました。こうして得られた10個の有理点のうち、8個は「辺の長さが 0 または負となる潰れた三角形の組」に対応し、残りの2個が共に上図の三角形の組に対応します。一方、Chabauty-Coleman法を実行する際の主な問題点は、代数曲線のMordell-Weil rank(※1)と呼ばれる量が種数よりも小さくなければならない、というものです。本研究では、2-降下法(※2)と呼ばれるコホモロジカルな手法によりMordell-Weil rankが1であることを証明することで、この問題点を克服しました。Case (2)も代数曲線の有理点集合の決定に帰着されますが、この代数曲線の有理点は全て「潰れた三角形の組」に対応します。

この初等的な定理の解決に用いられたChabauty-Coleman法と2-降下法は、共に1980年代以降に開発された比較的新しい数論幾何学の手法です。高度に抽象化された現代数学にも、このような身近な図形への応用例があることが分かりました。

※1 Mordell-Weil rank: 有理点を持つ代数曲線は、Jacobi多様体と呼ばれる高次元の代数多様体に標準的な方法で埋め込むことができる。Jacobi多様体の有理点集合は有限生成Abel群をなす (Mordell-Weil群)。このMordell-Weil群の rankをMordell-Weil rankという。例えば、Mordell-Weil rankが正であることとMordell-Weil群が無限群であることは同値である。

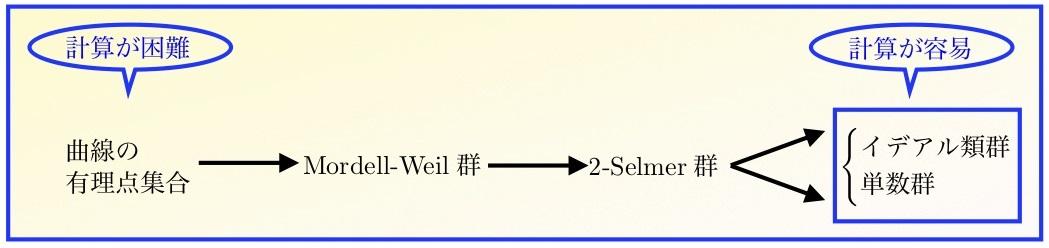
※2 2-降下法: Jacobi多様体のMordell-Weil rankの決定は、通常困難であるが、応用上はその上界（これより大きくないという値）を与えることさえできれば十分であることも多い。このような要請に基づき、Mordell-Weil群をコホモロジー群や2-Selmer群という計算が容易な「入れ物」に埋め込み、その「入れ物」の大きさを計算することで Mordell-Weil rankの上界を与える手法を2-降下法という。2-Selmer群の計算は、ある特定の代数体のイデアル類群や単数群というより古典的な不変量の計算に帰着される。現在では計算代数システムMAGMAに実装されている(cf. [Stoll])。

[Bremner] Andrew Bremner, On Heron triangles, Ann. Math. Inform. 33 (2006), 15–21. MR2385463

[van Luijk] Ronald van Luijk, An elliptic K3 surface associated to Heron triangles, J.Number Theory 123 (2007), no. 1, 92–119, DOI 10.1016/j.jnt.2006.06.006.MR2295433

[Coleman] Robert F. Coleman, Effective Chabauty, Duke Math. J. 52 (1985), no. 3, 765–770, DOI 10.1215/S0012- 7094-85-05240-8. MR808103

[Stoll] Michael Stoll, Implementing 2-descent for Jacobians of hyperelliptic curves, Acta Arith. 98 (2001), no. 3, 245–277, DOI 10.4064/aa98-3-4. MR1829626