メゾスコピックな箱に電子を閉じ込めるデバイスを「量子ドット」と呼びます。その箱の中で電子のエネルギーは飛び飛びの値(エネルギー準位)に量子化され、ミクロな原子と類似の性質を示すことから「人工原子」と呼ばれます [1]。電子はスピンという属性を持ち、それにはアップ\(\ \ket{↑}\ \)とダウン\(\ \ket{↓}\ \)の2つの状態があります。量子ドットに1個の電子を閉じ込めた人工水素原子におけるスピン状態は、アップとダウンの波としての重ね合わせ
\(C_{1}\)\(\ket{↑}\ \)+\(\ C_{2}\)\(\ket{↓}\ \) ( \(C_{1}\)、\(C_{2}\) は複素数で \(\vert{C_{1}}\vert^2 \) + \(\vert{C_{2}}\vert^2 \) = 1 )
(1)
\( \frac{1}{\sqrt{2}} \)(\(\ \ket{↑}\)\(\ket{↓}\ \)+\(\ \ket{↓}\)\(\ket{↑}\ \))
(2)
ここ数年、「ハイブリッド量子科学」という新分野が注目されています。電子の電荷とスピン、フォトン(光子)、フォノン(格子振動や微小な機械振動子の振動モードの量子)など、異なる量子系を組み合わせて新物性、新機能を探る研究です。大規模量子コンピューターの実現にはまだ長い時間が必要ですが、その実現に向けて蓄積されてきた技術に目を向け、幅広く有効に活用しよう、という発想が根底にあります。私は量子ドットの電気伝導、近藤効果などの基礎物性を理論的に研究してきました。ハイブリッド系としては、量子ドットを用いたフォノンレーザーの研究の他に、最近、量子ドットの光電流に着目しています。量子ドット中のエネルギー準位の間隔はテラヘルツ(THz)領域の光子のエネルギーに対応します。現在、THz電磁波の技術開発が非常に盛んです。量子ドットにTHz光を当てると電流が生じるため、その検出器に応用可能です(図(a))。2個の量子ドットを並べれば検出感度が2倍になりそうですが、実は量子効果を利用するとそれ以上の感度が期待できます。光の波長が量子ドット間の距離よりも十分長い場合、1個の光子の吸収によって式(2)のようなもつれ合いが生じ、次の光子の吸収率が増大する、これが高感度検出器の動作原理です(図(b))。量子力学には、未知の可能性がたくさん残っています。
[1] 江藤幹雄、「量子力学I」(丸善、パリティ物理教科書シリーズ、2013)、p.115、p.132
[2] 量子ビットとして電子スピンの他、原子核のスピン、光子(2つの偏光方向の重ね合わせ)など、様々な量子系が研究されている。「IBM Q」には超伝導回路の量子ビットが使われている。
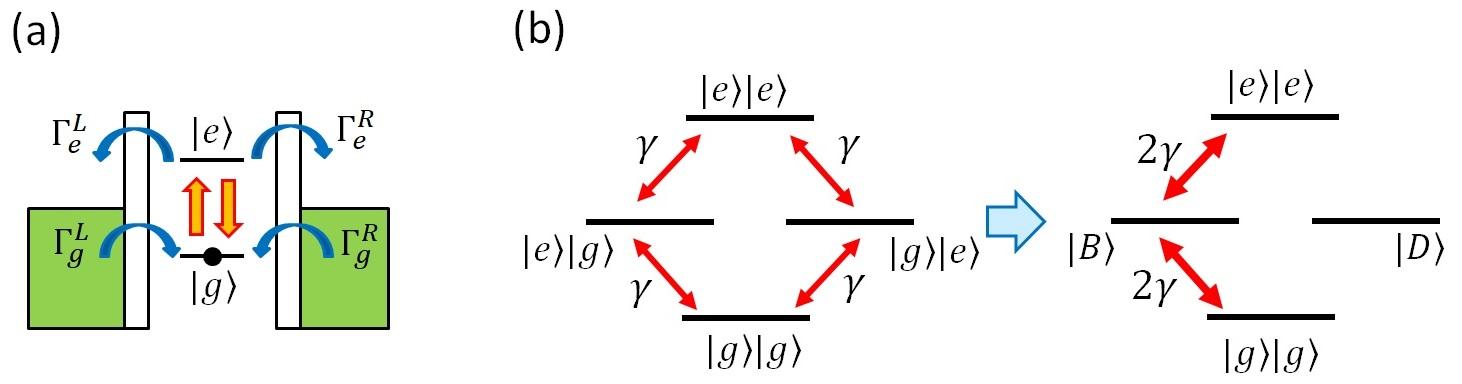
(a)量子ドットにTHz光を当てたときに生じる光電流の概念図。電子は光子を吸収すると、下のエネルギー準位(\( \ket{g} \))から上のエネルギー準位(\( \ket{e} \))に励起する。量子ドットの左右にはリード線がつながれていて、電子はポテンシャルの高い障壁を「トンネル効果」によって出入りする。トンネル率に非対称性があるとき( \(Γ^{L}_{g}\) / \(Γ^{R}_{g}\) ≠ \(Γ^{L}_{e}\) / \(Γ^{R}_{e}\) )、電流が生じる。
(b)2個の量子ドットを並べた時の光子の吸収率。量子ドット間の「もつれ合い」がないとき(左図)とあるとき(右図)。光の波長が量子ドット間の距離より十分長い場合、右図のように、光子の吸収によって\(\ \ket{g} \)\(\ket{g}\ \)から「もつれた状態」\(\ket{B}\ \)= (\(\ \ket{e} \)\(\ket{g}\ \)+\(\ \ket{g} \)\(\ket{e}\ \)) / \(\sqrt{2} \ \)が作られる。\(\ket{B}\ \)への遷移率は左図の2倍になり、もう一つの「もつれた状態」\(\ket{D}\ \)= (\(\ \ket{e} \)\(\ket{g}\ \)-\(\ \ket{g} \)\(\ket{e}\ \)) / \(\sqrt{2} \ \)への遷移は禁止される。


