序
数学というと厳密な値を正確に求め、そこに美しさを感じる学問というイメージを持っていると思いますが、それを如何に計算するかということも問題です。しかし、厳密な値を何らかの問題で計算できない場合もあります。そこで近似値を出すのですが、近似値というからには真の値との誤差が評価されているはずです。これから述べたいことは、積分表示を使った近似と誤差評価にも数学のアイデアと美しい世界が広がっているということです。
円周率 円周率 \( \pi\) は小学校では円形の筒の周りの長さを計って求めるのですが、これでは高い精度が期待できません。ギリシャ時代には円に内外接する正多角形の辺の長さからある程度の評価式が得られました。更に微積分が導入されてから、これから述べるような根本的に異なる近似方法が得られました。
三角関数 \( \tan \ x\) の逆関数は \( \arctan \ x\) と書かれます。高校数学で習った逆関数の微分公式を使うと積分表示
円周率 円周率 \( \pi\) は小学校では円形の筒の周りの長さを計って求めるのですが、これでは高い精度が期待できません。ギリシャ時代には円に内外接する正多角形の辺の長さからある程度の評価式が得られました。更に微積分が導入されてから、これから述べるような根本的に異なる近似方法が得られました。
三角関数 \( \tan \ x\) の逆関数は \( \arctan \ x\) と書かれます。高校数学で習った逆関数の微分公式を使うと積分表示
\( \arctan \ x \ = \ \int_0^x \frac{dt}{1+t^2} \)
が得られます。\( \arctan \ \frac{1}{\sqrt{3}} \ = \ \frac{\pi}{6} \) ですから、
\( π \ = \ 6 \ \int_0^{1/\sqrt{3}} \frac{dt}{1+t^2} \)
です。右辺の積分は(四則演算を使って)計算可能ではないことが知られていますが、等比級数の和公式から
\( | \frac{1}{1+t^2} - \left( 1-t^2+t^4-t^6+ \ \cdots \ + \left( -1 \right)^nt^{2n} \right) | \ = \ | \frac{ \left( -t^2 \right)^{n+1} }{1+t^2} | \ \leq \ t^{2n+2} \)
となり、評価式
\( | \pi-2\sqrt{3} \left( 1-\frac{1}{3 \cdot 3}+\frac{1}{5 \cdot 3^2}+ \ \cdots \ + \left( -1 \right)^n \frac{1}{ \left( 2n+1 \right) 3^n} \right) | \ \leq \ \frac{ 2 \sqrt{3}}{ \left( 2n+3 \right) 3^{n+1}} \)
が得られます。左辺に現れる級数和を \(S_n\) として実際に計算してみます。

言うまでもなく、\( \pi\) の積分表示を得ることによって微積分などの道具が使えた訳ですが、その有効性は想像以上ではないでしょうか。(実は\( \ \sqrt{3} \ \) を先に計算することを前提としていますが、有理数だけで近似する方法も知られています。)このような積分表示の有効性は幾何的なものに限りません。
破産確率 A 君の全財産は 100 円です。これからコインを投げて表が出ると 100 円取得し、裏が出ると 100 円失うゲームをします。全財産を失うとゲームは終了します。このとき、全財産を失わない確率を求めましょう。
1 回目でコイン投げで勝つ確率は\( \ \frac{1}{2} \ \)です。したがって、全財産を失っていない確率は\( \ \frac{1}{2} \ \)です。
2 回目のコイン投げでは、1 回目でコイン投げで勝っていれば、全財産を失わないので、全財産を失っていない確率も\( \ \frac{1}{2} \ \)です。
3 回目のコイン投げでは、2 回目でコイン投げで勝っていれば、負けてもよいですが、2 回目でコイン投げで負けていれば、勝たないと全財産を失います。したがって、3 回目まで全財産を失っていない確率は
破産確率 A 君の全財産は 100 円です。これからコインを投げて表が出ると 100 円取得し、裏が出ると 100 円失うゲームをします。全財産を失うとゲームは終了します。このとき、全財産を失わない確率を求めましょう。
1 回目でコイン投げで勝つ確率は\( \ \frac{1}{2} \ \)です。したがって、全財産を失っていない確率は\( \ \frac{1}{2} \ \)です。
2 回目のコイン投げでは、1 回目でコイン投げで勝っていれば、全財産を失わないので、全財産を失っていない確率も\( \ \frac{1}{2} \ \)です。
3 回目のコイン投げでは、2 回目でコイン投げで勝っていれば、負けてもよいですが、2 回目でコイン投げで負けていれば、勝たないと全財産を失います。したがって、3 回目まで全財産を失っていない確率は
\( \frac{1}{2} \times \left( \frac{1}{2} \times 1 + \frac{1}{2} \times \frac{1}{2} \right) \ = \ \frac{3}{8} \)
です。
4 回目まで全財産を失っていない確率も\( \ \frac{3}{8} \ \)です。同様にして、全財産を失うのは奇数回です。
一般に 2\(n\) 回目まで全財産を失っていない確率は
4 回目まで全財産を失っていない確率も\( \ \frac{3}{8} \ \)です。同様にして、全財産を失うのは奇数回です。
一般に 2\(n\) 回目まで全財産を失っていない確率は
\( p_{2n} \ = \ 2^{-2n} {}_{2n} \mathrm{ C }_n \ = \ \frac{ \left( 2n-1 \right) \left( 2n-3 \right) \ \cdots \ 1}{2n \left( 2n-2 \right) \ \cdots \ 2} \)
であることがわかります。(証明はやや面倒なので、省略します。)これは厳密な値ですが、今度は計算が容易ではないです。例えば、
\( p_{100} \ = \ \frac{ \ 99 \cdot 97 \cdot 95 \ \cdots \ 1 \ }{ \ 100 \cdot 98 \cdot 96 \ \cdots \ 2 \ } \)
です。しかし、本当に欲しいのはおおよその値ではないでしょうか。
ここでも積分表示が役に立ちます。数学的帰納法から容易に
ここでも積分表示が役に立ちます。数学的帰納法から容易に
\( p_{2n} \ = \ \frac{2}{ \pi} \ \int_0^{ \pi/2} \sin^{2n}tdt \)
であることがわかります。これと相加相乗平均を使ったほんの少しの議論から評価式
\( \sqrt{ \frac{4n+4}{4n+3} } \frac{1}{ \sqrt{ \pi \left( n + \frac{1}{2} \right)}} \ \leq \ p_{2n} \ \leq \ \sqrt{ \frac{4n+1}{4n} } \frac{1}{ \sqrt{ \pi \left( n + \frac{1}{2} \right)}} \)
が得られます。したがって、\( n\ \)が十分大きいとき、\(p_{2n}\ \)は\( \ \frac{1}{ \sqrt{\pi n}} \ \)に近い、式で表すと
\( p_{2n} \ \fallingdotseq \ \frac{1}{ \sqrt{\pi n}} \)
です。これを検証してみましょう。
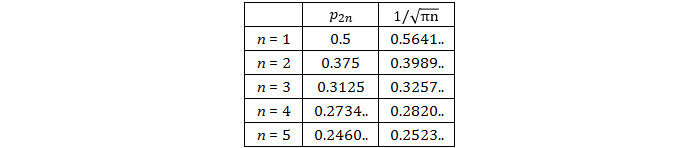
\( n\ \)が小さいときは精度が高くないですが、真の値が計算できます。一方、\( n\ \)が大きいほど精度が上がりますので、\( p_{100}\ \)は\( \ \frac{1}{ \sqrt{50 \pi} }\ = \ 0.07978.. \ \)にかなり近いはずです。勿論、誤差評価もできます。(逆に考えると、何らかの実験データから、\( n\ \)が非常に大きいとき、確率が近似的に\( \ \frac{1}{ \sqrt{\pi n}} \ \)であることがわかっても、本当に何が起こっているのかを理解できず、\( n\ \)が小さいとき、誤差が問題となる可能性があります。)
まとめ 積分表示の有効性は上記の例をはるかに超えて、現代数学の至る所に現れています。また、数理物理学における(経路)積分表示を使った計算は驚くべきものです。一方、破産確率のように経済活動、日常生活に現れる問題にも応用することができます。但し、積分表示は中間目標のようなもので、その前に現れる状況の数式化、その後の数式の取扱いの両面を理解しておく必要があります。数学を学ぶとはそういうことです。
まとめ 積分表示の有効性は上記の例をはるかに超えて、現代数学の至る所に現れています。また、数理物理学における(経路)積分表示を使った計算は驚くべきものです。一方、破産確率のように経済活動、日常生活に現れる問題にも応用することができます。但し、積分表示は中間目標のようなもので、その前に現れる状況の数式化、その後の数式の取扱いの両面を理解しておく必要があります。数学を学ぶとはそういうことです。


