最近、金融工学などの影響でマルチンゲールという用語をよく耳にするようになったと思います。マルチンゲールは、次のような性質を持つ確率過程の一種です。
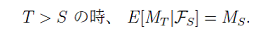
左辺は、時刻 \( S \) までの \( M_t \) に関する情報\( F_s \) が与えられた時の条件付き期待値を表します。つまり、現在の時刻\( S \)までのことがわかったときに 未来の時刻 \( T \) のことを予測して期待値を計算すると、現在の値になる、ということになります。典型的な例は、公平な賭で得る儲けです。数学的には、単純ランダムウォークやブラウン運動などが典型的な例になりますが、それらを含むずっと広範な確率過程の種類となります。Doob はこの確率過程と関数論でよく知られている調和関数が似ていることを発見しました。Δをラプラシアンとすると、Δ\(u=0 \)を満たす関数を調和関数といいます。これら二つの定義式だけを見ても似ているようには全く見えませんが、マルチンゲールの方に任意停止定理を使うと、
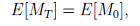
実平面上の場合、調和関数に(調和関数の)平均値の定理を使うと、
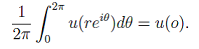
つまり、時刻 \( T \) の時に(半径 \( r \) の円周上で)平均を取ると、時刻0 (円の中心)での値が出るということです。こんなちょっとした見た目だけで似ていると喜んでいるのは、数学者と云うのは本当に暢気なものだな、と思われるかもしれません。重要な点は、見た目だけではなく数学的構造として密接な関係がある、ほとんど同じようなものだ、ということです。実際、調和関数は、ほとんどマルチンゲールと考えてもよいということがわかります。これには重要な仲介役、ブラウン運動が必要です。平面上のブラウン運動\( X_t \) を調和関数 \( u \) に代入したもの、\( u(X_t) \) を考えると、これはマルチンゲールになります。つまり、マルチンゲールという確率過程の種は調和関数という関数の種を含んでいると見ることができます。調和関数を調べるには、マルチンゲールを調べれば良い、ということになります。Doob 以降、マルチンゲール理論は活発に研究されましたが、マルチンゲール理論をはじめとする確率論の議論を使って調和関数について多くのことがわかりました。また、仲介役としてブラウン運動がいましたが、このような研究ではブラウン運動をはじめとする拡散過程の理論が大きな役割を果たしていることも付け加えておきます。これによって、多様体上やフラクタル集合など特異な空間上の調和関数についても調べることが可能となりました。
さて、全く別の分野から、もう一組の似た者同士を紹介しましょう。
複素平面\( C \) 上で z= x+\( \sqrt{-1} \) y の複素共役で微分すると 0 になる関数を正則関数といいますが、共通零点を持たない正則関数の比で表される関数を有理形関数といいます。有理形関数の取りうる値の様子を調べる理論として、ネヴァンリンナ理論があります。Vojtaはこのネヴァンリンナ理論と数論のディオファントス近似論で知られているRothの定理が似ていると言い出しました(1987年)。その一部を見てみましょう。
『R. Nevanlinnaの第2主定理(1925年):
任意の定数でない有理形関数\( f\)と相異なる点\( a_1,…,a_q\)ϵC∪{∞}に対して
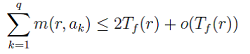
が0< \( r \)に関して長さ有限の集合を除いて成り立つ。』
ここで、\( m\)(\(r, a_k\))は\( f\)の像と点 \( a_k \)の「近さ」を測る関数、\( T_f \)(\(r\))は\( f\)の像の「大きさ」を測る関数で、
\( T_f \)(\( r \)) ↑∞ (\( r \)↑∞)を満たします。
『Rothの定理(1955年):\( α \)が代数的な数ならば、任意の ϵ>0 に対して、
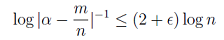
が、有限個の組を除く任意の互いに素な整数 \( m,n \) (\( n\)>0) について成り立つ。』
代数的数とは有理数係数の代数方程式の解になっているような数です。左辺は、\( α \)を有理数 \( m/n \) で近似するときの「近さ」を表しますが、それが右辺で有理数のある種の「大きさ」によって制限を受けることを示しています。確かに似たような関数の関係式と見え、右辺には "2"が現れています。ここには、マルチンゲールと調和関数の時のように直接的な接点は考えられませんが、多くの共通点が知られています。因みに、L. Ahlfors は、Nevanlinnaの定理の右辺の"2"について球面(≅C∪{∞}) のオイラー数が現れていることを見出しています。 上のことはより一般的に述べることができ、数論で注目されているディオファントス近似の式と関数論の基本的な不等式に類似がある、ということで、多くの数学者を刺激し、研究を促進しました。Vojta以降、正則写像の研究を通して数論的問題に挑戦するという試みも多くなされ、この発見は複素解析、複素幾何、数論に大きな影響を与えました。
私自身は、ネヴァンリンナ理論と、正則関数・有理形関数の確率論的類似として知られる正則マルチンゲールの関係に注目しています。これを用いると、広いクラスの複素多様体上の有理形関数に対してもネヴァンリンナの第2主定理の類似が成り立つことを示すことができます。さらに、Vojtaの発見に関連して見ると、ランダム正則関数についてどうなるかとか、ネヴァンリンナ理論の最良性との関係とか、ディオファントス近似とネヴァンリンナ理論の間には馴染みのある「仲介役」はいないかとか、妄想はどんどん膨らんでいきます。妄想だけでは何もなりませんが。兎に角、数学では全く違った分野から似た者同士を見つけるというのは、数学を動かす原動力になるものだと思います。


