わたしたちは学校で数の世界のひろがりを教わりながら成長します。風呂につかって300まで数え、分数、負の数、無理数となっていくに従って、出来ることがどんどん増えるので楽しい気分になります。複素数までならうと、どんな2次式でもかならずふたつの1次式の積に分解出来ることに満足した人もきっと多いでしょう:
\( x^2+1=(x-i) \cdot (x+i), i^2=-1\)
また複素数全体は複素平面を通じて、いつの間にやら2次元的な形をもったものとして、その上で解析ができることも実はすごいことです。

”整数\( a,b \)の平方の和でかける整数\( n = a^2+b^2 \)はどんなものか?”という整数の問題があります。すこし実験してみれば、\( 2 = 1^2 + 1^2 < 3 < 1^2 + 2^2 = 5\) なので\( 3 \) はムリだけど\( 2 \) や\( 5 \) は出来る、などの区別が観察されます。従って問題にしたい気持ちもわかるところですが、これも\( i = \sqrt{-1} \) を使って考えるとぐんと景色が深まります。
素因数ごとに考えればよいので\( n \)は素数\( p \)として、すると問題は整数\( a \)、\( b \)があって
\( p = a^2 + b^2 \) と和にかける素数 \( p \) はどんなものか?
ということですが、これに皆さんはどうやって \( i \) をつかいますか。
これはまず上を
\( p = (a + ib) \cdot (a - ib) \) と積にかける素数 \( p \) はどんなものか?
というふうに読みかえるのです:

そして、もちろん\( a + ib \) や\( a - ib \)はもはや普通の整数ではないですが、普通の整数 \( a \) や \( b \) や \( i \) と組み合わせてできる進化した整数なのだ、というふうに思いきって発想をジャンプします。するとつまり「うまい新しいタイプの整数をつかって改めて素因数分解を考えなおしてみたら、世の中どうなるだろう」と自然にいくらでも拡がってくる。ただ闇雲に解答するより、明らかに事実のツボをおさえたことになります。わたしはこれを学生のときに教わって、自分で編みだしたのでないのは残念でしたが、それでもなにか数学の自由さ(だって素数の素因数分解をするのだから)を感じた楽しい瞬間のひとつでした。
すこし発展的になるかもしれないですが、いまの場合は答えもふるっています。実際、求めたい素数全体は
\( f(x) = x^2 + 1 \) に \( x = 1,2,3,\ldots,n,\ldots \) を代入して出来る自然数 \( f(n) \)
の素因数分解に出現する素数達全体、にも丁度一致するのですが、それは
\( 4 \) で割ると\( 1 \) 余る素数たちのきっかり全体、
例えば \( 5 = f(2) = (2+i) \cdot (2-i) \) など, とあとそれに \( p = 2 \) をあわせて、すべて与えられることがわかります。要するに”法則”があるのです。これは\( \pm i \) が \( x^2+ 1 = 0 \) の根であり、また \( i^4 = 1\) だから奇素数 \( p \) に対して
\(
i^p =
\begin{cases}
\ \ \ i \ (p \equiv 1 \mod 4)\\
-i \ (p \equiv 3 \mod 4)
\end{cases}
\)
であることから導くことが出来ます。
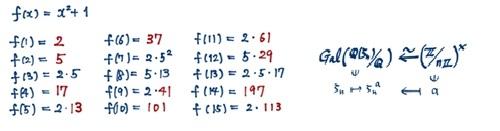
この法則が成立する根本的な理由は、\( i\)がそれぞれ代数的には\( i^4=1\)であること、幾何的には複素平面内の単位円の4等分点を与えること、そして解析的には \( i = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \) として三角関数に関係すること、とまとめられます。3つの視点は区別はありますが、お互いもっともらしく関係していることは少し知識があればわかりますね。また円周の等分というような規則正しさが、素数の分解の規則正しさにつながるというのもちょっと不思議ですが、まあありえる話かなと感じる人もいるでしょう。数学ではもっと複雑玄妙な規則正しさもあり、それが上のように別のことに思いがけずつながっていることが時々見つかります。自由な発想と観察でそういったことを探してみると面白いです。


