都市には、様々な種類の施設が存在します。飲食店やスーパー、銀行のATMや郵便局など身近なものから、学校、病院、消防署や市役所など、公共的なサービスを提供するものまで多種多様です。こうした施設の配置場所は、どのような仕組みで決められているのでしょうか。施設の位置によって、サービス利用者の利便性や、店舗の売り上げが大きく異なるはずです。
与えられた空間において、施設の望ましい配置場所を見付ける問題は、古くから多くの研究者が取り組んできた魅力的なテーマです。ここでは、この問題を、私の専門のオペレーションズ・リサーチ(OR)という学問分野で研究されている数理モデルの一つである「施設配置問題」を取り上げて、紹介したいと思います。
施設配置問題は、対象空間において、利用者の居住地の集合と、施設の配置候補地の集合が与えられた下で、施設の望ましい配置場所を決める問題です。施設の種類や、施設配置の評価尺度に応じた多くの種類が存在します。例えば、最大カバー問題とよばれる施設配置問題は、施設から一定距離以内に居住する利用者(カバーされた利用者)の総数を最大化する施設の配置方法を決める問題です。
ところで、施設配置問題は、空間的な意思決定モデルであって、多くの場合、時間の流れは完全に無視されます。ところが実際には、施設サービスに対する需要は一日のなかでも大きく変化します。また、施設も(コンビニエンスストアなどの一部の例外を除き)一日中オープンしているわけではありません。そこで、施設配置問題に時間的要素を組み込んで、一つ次元を上げた時空間領域における最適なサービス提供方法を決める問題を追求することには、学術的にも実際的にも大きな価値がありそうです。後半部では、私が取り組んだそうした試みの一部を紹介します(詳しくは最後の文献[1]をご参照ください)。
図1は時空間領域とそのなかでの人の流れを表しています。この図の水平断面は、鉄道網や道路網などの物理的空間を、垂直軸は時間軸を表しています。ここでは、就業後に勤務地から鉄道を使って帰宅する途中の駅にある施設に立ち寄る状況を想定しましょう。例えば、クラシック音楽のコンサートを聴きに行く、といった場面です。もちろん、英会話スクールや学習塾、映画やスポーツ観戦などに置き換えることもできます。サービス提供者の最大の関心事は、多くの人にサービスを利用してもらうことでしょう。その際に、施設を配置する駅の選定はもちろん重要ですが、サービスを開始するタイミングも非常に大切です。サービスの開始時刻が早すぎると退社後に開始に間に合う人が、そして逆に遅すぎるとサービス終了後に帰宅可能な人が減ってしまうため、いずれの場合においても潜在的な顧客を十分に確保できないのです。
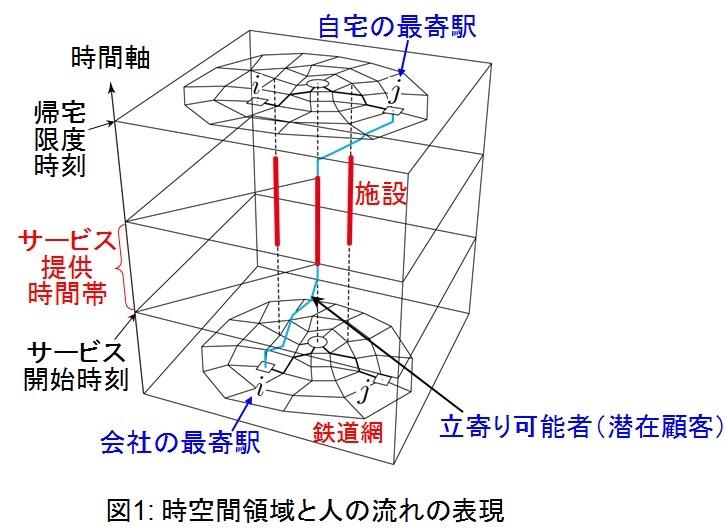
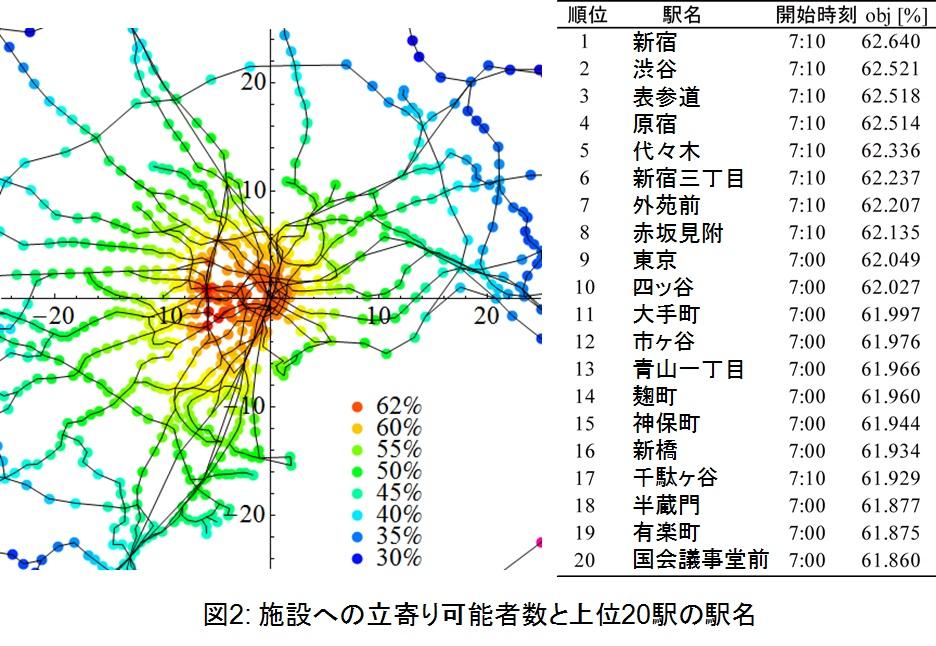
図2は、実際の鉄道流動データを用いて計算した首都圏の鉄道駅における立ち寄り易さを表しています。各駅の値は、施設をその駅だけに一つ配置し、最適な開始時刻を選択した場合の結果で、退社後に施設に3時間立ち寄り、23時までに帰宅可能な人数(全移動者数に対する割合)を表しています。図の原点は東京駅で、単位は1kmを表します。立ち寄り可能者数が最大なのは新宿駅で、渋谷など新宿駅に近い駅や、東京駅周辺の駅が際立って見えます。こうした駅付近に多くの施設があるのも納得できるのではないでしょうか。
次に複数の施設を同時に配置する場面を考えます。同一の経営主体がチェーン展開する店舗を複数配置するような状況です。ここでの問題は、配置された施設のどれか一つには立ち寄ることが可能である利用者を考え、この総数を最大化するように、各施設の配置駅と開始時刻を決定する問題です。施設が複数になると、すべての解を列挙して最良の計画案を見付けるという方法では、最速のコンピュータをもってしても事実上不可能です。そこで、与えられた解を改善する手続きを繰り返す解法をコンピュータプログラムとして実装し、得られた結果を紹介します。
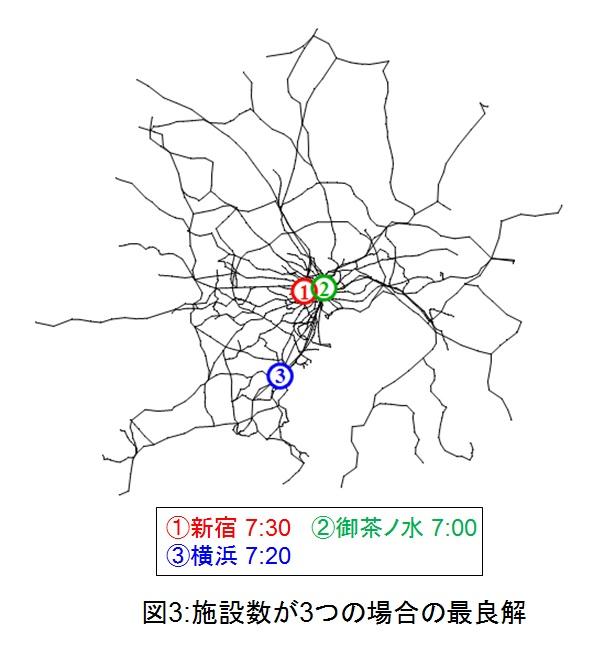
図3は、施設数が3つの場合の結果で、新宿と御茶ノ水と横浜が選ばれています。新宿と御茶ノ水という非常に近接した駅が選ばれており、開始時刻が30分も異なっている点が大きな特徴です。時間軸を無視した場合には、近接した二つの駅を選択するメリットはありません。しかし実際には、多くの人が立ち寄り易い都心部に施設を同時に配置し、サービス開始時刻に差を付けることで、時空間的に異なる性質の人々の流れを効率的に捉えることができるのです。このように、空間的な意思決定問題に時間軸を導入することで、数多くの新しい展開が期待できそうです。
近年、大規模かつ詳細な地理データが様々な形で公開されています。また、情報通信技術の進展により、人々の実際の行動履歴に基づく大規模な流動データを整備する試みもなされています。こうした状況の下では、現実をモデル化する方法論をも研究対象とするORの活躍の場は、今後ますます広がっていくものと考えています。
参考文献
[1] K. Tanaka: Maximum flow-covering location and service start time problem and its application to Tokyo metropolitan railway network. Journal of the Operations Research Society of Japan,Vol. 54-4, 2011, pp. 237-258.


