スウェーデンのアクチュアリーであったLundberg, F. やCramér, H.は、100年以上前に、保険会社の持つサープラス(余剰金)に対するモデルとして次のような式を提案しました。このモデルは、古典的リスクモデルとかCramér-Lundbergモデルと呼ばれていて、危険理論(risk theory)における最も基本的なモデルと言われています。
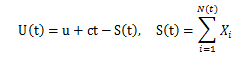
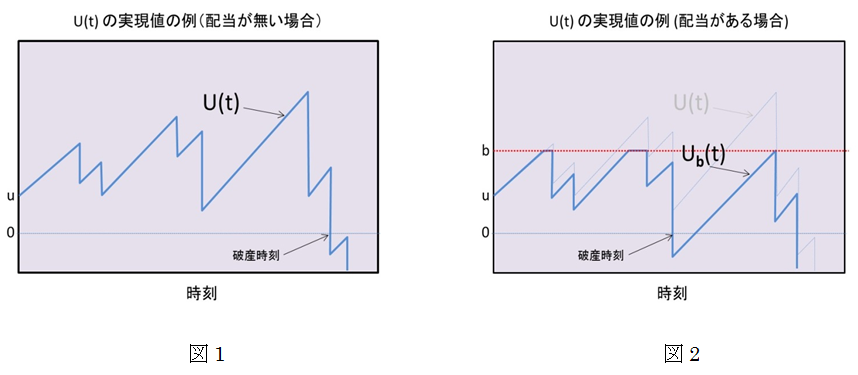
ここに、U(t)とは時刻tにおけるサープラスの額で、uは初期サープラス、cは保険料率を表す正の定数、S(t)とは時刻tまでの保険金支払総額を表しています。つまり、このモデルでは、単位時間当たりcの保険料収入があり、それが、サープラスの増加に寄与しています。一方で、保険金支払により、S(t)だけサープラスの減少に影響を及ぼしていると言えます。さらに、右側の式を見てみると、N(t)とは時刻tまでの保険金請求頻度を表し、Xiとは第i番目の保険金支払金額を表しています。つまり、保険金支払総額S(t)には、頻度に関わる不確実性と支払金額に関わる不確実性という2種類の‘不確実性’が含まれており、複合ポアソン過程と呼ばれる確率モデルの1つとして知られております。 この古典的リスクモデルを応用した研究分野の1つに、株主配当問題についての研究があります。具体的には、図1のようなU(t)の実現値に対し、配当境界(dividend barrier)と呼ばれる境界値bを設定し、U(t)がbを上回る部分を配当として株主に返還するという新たなモデルを考えます(図2を参照)。この境界値bについて考えると、bの水準が低いほどより早期に配当が得られて有利に感じますが、一方で、bの水準が低いほど早期にU(t)<0となる(このモデルでは、この現象は保険会社の倒産を意味します。)リスクが増加します。逆に、bの水準が高いほど早期の倒産リスクは減少しますが、配当を享受するチャンスが減少します。このようなトレードオフの関係の中、De Finetti などは、最適配当境界(optimal dividend barrier)として、破産時刻Tまでに支払われる配当の現在価値の期待値
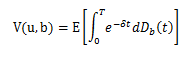
が最大となるような境界値を提案しました。
前置きが大変長くなってしまいましたが、私の研究内容は、この最適配当境界を統計的に推定することが目的です。このモデルにおける確率変数である保険金請求頻度N(t)や保険金支払金額Xiの分布は一般には未知であり、最適配当境界を計算するためには何らかの推定が必要になります。実際に観測できるデータの関数として、この最適配当境界の推定量を提案し、その推定量の良さ(真の最適配当境界とどれだけ近いか?)を評価するのが現時点での私の興味の1つです。