微分方程式を解く

『自然現象は方程式で記述されます』と言われたら皆さんはどう思いますか？ 風でざわめく森の木々や、波打ち際でしぶきを上げて砕ける波を見ていると、その細部では非常に複雑な挙動をしていることが分かります。そのような複雑な運動を方程式が記述するなど、にわかには信じられないかもしれません。しかし、その現象の裏に潜んでいる基本原理を見出し、それを数学の言葉で表すことにより方程式が得られます。自然現象を記述する方程式の多くは微分方程式になります。

現象を定量的に予測するためには、得られた微分方程式を解かなければなりません。ところが、この『解く』という言葉は人によりあるいは問題設定によりその意味が異なり、不用意に『解いた』などと言うと、ちぐはぐな議論になりかねません。理工学部の１年次に習う定数係数線形の常微分方程式は、高校までに習った指数関数、三角関数などの初等関数を用いてその解を表示することができます。そのような表示を得ることを初等的に解くといいます。これが変数係数の常微分方程式になると、初等的に解けるのはごく稀になってしまいます。初等的には解けないが物理学でしばしばでてくる重要な微分方程式に対しては、その解を新しい関数として定めたりします。例えば、Besselの微分方程式

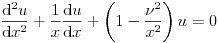
の解としてBessel関数が定義されます。νが自然数の場合、この関数は次のようにべき級数で表示されます。

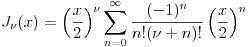
このような関数は特殊関数と呼ばれ、初等関数や特殊関数で表示される解があるとき、その方程式は厳密解をもつといいます。上の表示では、初等関数を無限個足し合わせています。線形の方程式に対してはこのような手法はよく使われ、熱の拡散を記述する熱伝導方程式の解は、ある特別な問題設定の下で次のようなFourier級数で表示されます。

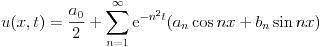
このように解の表示を得る方法は幾つもあるのですが、その意味で解ける微分方程式は、微分方程式全体の中でごく僅かしかありません。

工学において必要になるのは、解の数値です。解の表示が得られていれば比較的簡単にその数値が得られますが、解の表示がなくてもその数値を近似的に求めることはできます。差分法、有限要素法、スペクトル法などの手法を用いて方程式を離散化し、コンピュータを使って数値計算を行い離散的な数値解を求めるのです。コンピュータの性能の飛躍的な向上により、近年、数値解析は重要な役割を担っています。このような数値解を求めることも、方程式を解くという範疇に入ります。しかし、ただ闇雲に数値シミュレーションを行えばよいというものではありません。数値計算においては有限回のステップで計算が破綻してしまう場合がありますし、その破綻を強制的に押さえるような計算手法もあります。そうなると、真の解の近似値を得られているか怪しくなります。そもそも真の解と呼べるようなものがあるのでしょうか？それに答えるのが解の存在定理であり、それを示すためには数学が重要な役割を果たします。さらに数学の抽象理論を使えば、解の表示を用いなくても方程式から解の性質を導き出すことが可能になり、また方程式を離散化して得られる近似解の近似の精度を議論することもできます。このような存在定理や解の挙動を証明することも方程式を解くという範疇に入ります。

この最後の意味で解けていない重要な方程式としてNavier‐Stokes方程式があります。

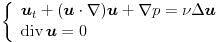
これは液体のような非圧縮粘性流体の基礎方程式であり、乱流をも記述すると信じられています。1934年のLerayによる数学的な研究以来、多くの数学者によって調べられていますが、その滑らかな解が時間大域的に存在するのか、あるいは有限時間で解の値が無限大に発散するような爆発現象が起きるのかは未解決です。このような未解決問題を解くために日々、新しい手法、新しい数学が生み出されています。