藪野 浩司 (機械工学科 教授)
機械システムに存在する非線形性の積極的な利用という新しい考え方を通して、真に人間の役に立つ工学システムを作り出すために、大学で身につけておくべき学問とはどのようなものかを考えてみたい。
1. 線形と非線形
ほとんどの機械システムは非線形性をもつ。たとえば振り子の復元力は角度のsinに比例し、角度に比例しない(すなわち非線形)。この非線形性によって、最も単純な機械システムである振り子でさえも、その支点を周期的に加振すると未来の状態予測が不可能なカオスを生じる。 小学校からそれぞれのレベルに応じて再三取り上げられる、おなじみの振り子とばね‐質量系(図1)の運動を通して、システムの非線形とはどのようなものか見ていこう。ばね-質量系の運動方程式ma=F(m:質点の質量、a:質点の加速度、F:質点に加わる外力)は
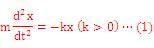
である。ここで特に注目すべきことは右辺のxの係数が負であることであり、質点の変位に対してばねはそれとは逆向きに力(すなわち復元力:質点がばねを正の向きに引っ張るとばねはそれとは逆向きに(負の向きに)質点を引っ張り返す力)を質点に及ぼすことを意味する(この関係は図2のように右下がりのグラフで表される)。
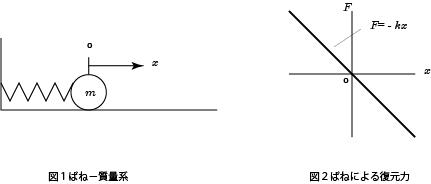
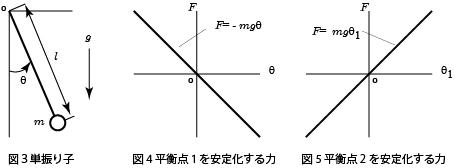
一方、図3に示すような振り子の運動方程式は以下のようになる。
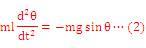
ばね‐質点系のそれと比べてみよう。ばね‐質点系では外力(F=-kx )が変位xに対して比例する(このような力を線形な力という)のに対し、振り子では F=-mgsinθのように角度 に比例しない(このような力を非線形な力という)*1。
2.平衡点と安定性
次に上に示した運動方程式から、振り子の平衡点(要するに釣り合の状態)を導いてみよう。平衡点とは時間がたっても変化しない状態であるから、運動方程式に対して「時間に関する1階微分と2階微分が0」という条件を課したとき(ここでは運動方程式の左辺の角加速度を0とおいたとき)に満足される状態(角度)である。すなわち
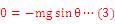
をみたす角度が平衡点であり、振り子は平衡点を二つ (θ=0とθ=π:平衡点1と平衡点2と呼ぶことにする)持つことがわかる。平衡点を一つ(x=0)しか持たないばね‐質量系とは異なり、振り子は外力の非線形性によって複数の平衡点を持つ。もちろん、θ=0は重力方向を向いた姿勢であり、θ=πは倒立姿勢である。
高校までの物理では、「振り子の角度は微少であると仮定して」という条件のもとに、sinθ≒θという近似(θ=0の近くで成り立つ、sinθの近似式:sinθをθ=0のまわりでテイラー展開してθの1次の項まで考慮する近似)が行われる。この結果外力はθに比例して(図4参照)、運動方程式(2)は
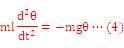
のように近似され式(1)と等価になり、近似が成り立つθ=0の近く|θ|≪1では、ばね‐質点系と同様な単振動をすることがわかる。しかしながら、はじめからこのように近似された(線形化された:非線形性が無視された)運動方程式を対象としていたのでは、平衡点は一種類(θ=0)しか求められず、倒立姿勢(θ=π)が平衡点であることを見い出すことはできない。
ところで、二つの平衡点θ=0.θ=πは明らかに異なる物理的性質をもつことを我々は感覚的に知っている。すなわち振り子を重力方向に向けてその状態を保つことは容易であるが、倒立姿勢を保つことは非常に難しい。この違いはどこから来るのだろう。上述の「平衡点」という概念からはこれに答えることはできず、「安定性」という概念が必要になる。振り子の運動方程式(2)を近似せずに解けばよいのだが、残念ながら初等関数で厳密解を書くことはできない*2。そこで倒立状態の近くで成り立つ近似式を考える。今度は θ=πの近くで成り立つsinθの近似式、すなわちsinθのθ=πまわりでのテイラー展開式
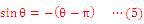
により、振り子の運動方程式(2)は倒立状態の近く|θ-π|≪1で以下のような線形化された式に変形できる。
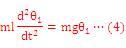
ここで、θ-π=θ1とおいた。すなわち、θ1は倒立状態からの角度である。右辺で示される外力を図2と同様に表してみると、右上がりの図5になる。ばねで考えれば、質点がばねを正の向きに引っ張るとばねはそれと同じ向き(正の向きに)質点を引っ張り返すようなばねである(実際にはそのようなばねは存在しないが)。従って式(4)の右辺で表される力は、倒立状態からの角度θ1を0にもどす(倒立状態に戻す)力ではなく、θ1の大きさをより大きくする様な力で、振り子には倒立状態から離れようとする力が働いていることが分かる。このような状態を「不安定」という。*1すなわち、倒立状態は不安定な平衡点ということになる。
3.非線形現象の利用
一般に機械システムは振り子に比べてさらに複雑な非線形性を持ち、(複数の平衡点が存在し、それらの安定性も様々で、)予測不可能な非線形挙動を示す可能性がある。安全性や信頼性を確保するために、非線形挙動が生じないよう、高剛性な(その結果重量化してしまう)機械システムが、狭い動作範囲(振り子でいえば近似sinθ≒θが成り立つ狭い動作範囲)で利用されてきた。しかしながら近年の、機械システムの高機能・高機能化への期待は、柔軟化・軽量化や非線形挙動が生じるような広い範囲(振り子でいえば近似sinθ≒θが成り立たない範囲)への動作拡張を要請し、もはや無視できなくなったシステムの非線形性といかに向きあい、安全性や信頼性を確保し続けるかが重要な課題になっている。
このような状況の中、これまでの発想とは逆に*3、元々システムに内在する非線形性によって生じる非線形現象の複雑性や多様性(振り子でいえば複数の平衡点の存在とその安定性の違い)を積極的に利用して、従来不可能であった運動制御を可能にしようという試みが注目されつつある。そのいくつかを紹介しよう*4。自由度の数に比べてアクチュエータの数が少ないマニピュレータを劣駆動マニピュレータと呼ぶが、非線形現象を発現させそれを積極的に利用することで、フィードバック制御なしに、運動制御が可能になる
http://youtu.be/tP88f-SwO_E
。また、鉄道車両が高速走行時に発生する蛇行動という共振現象をジャイロ効果によって安定化する方法
http://youtu.be/hGlZ8mWGkuM
や、生体試料観察には必要不可欠な原子間力顕微鏡(AFM)で使われるマイクロカンチレバーのナノメータスケールでの振幅制御も、非線形現象を積極的に用いることによりはじめて可能になった例である。
4.工学における役に立たない(?)学問のすすめ
特に工学を志す学生から、「1年生で学ぶ数学や物理が何の役に立つかわからない」という言葉を聞くことがある。上記のように非線形性を積極的に利用するには、役に立たないと思われている*5学問のその先にある最先端の数学や物理を道具として自由自在に使いこなす必要がある。数学や物理学が提供するものは物事の真理であり、工学にとってはある意味コンピュータよりもはるかに有用な道具であろう。そしてそれらは真理であるから流行り廃りもせずいつの時代も通用する普遍的な考え方を与えてくれる。
目まぐるしく変遷する時代のニーズを的確にとらえて新たな工学システムを生みだしていくためのブレークスルーは、これまでの工学の考え方や方法にいくら接ぎ木をしていっても生まれないだろう。真理を提示してくれる数学や物理学などの基礎学問に立ち帰かえり、その最先端の考え方を道具として使いこなす必要がある。一見何に役に立つかわからないと思われている基礎学問に立脚した工学の基礎をしっかりと身につけ、企業とは異なり利益を上げる必要がない大学だからこそできる10年・20年後を見据えた工学の基礎研究を行い、社会に出て真に人間の役に立つ工学システムを作り出してもらいたい。
*1 厳密な定義は専門書を参照してください。たとえばV.I. Arnold, Mathematical Methods of Classical Mechanics, 1988, Springer
*2 楕円関数を使えば解析的に解ける
*3 従来の発想に従えば、システムに内在する非線形性に起因した複雑現象の発生をいかにして抑えるかを考えることになる。
*4 実験結果のみを映像で紹介するが、適用された制御方法は運動方程式(非線形常(偏)微分方程式)をたてそれを非線形解析することによって、考え出されたものである。
*5 もちろん役に立つ


