「あるパーティーで、各出席者が握手した回数の総和をとると必ず偶数になる」
これはグラフ理論の最初に登場する「握手補題」と呼ばれる定理です。グラフとは、図1のように、いくつかの頂点とそれらを結ぶいくつかの辺からなる構造のことです。最初に述べたパーティーで握手の回数を考える問題では、パーティーの出席者を頂点とし、握手をした2人を辺で結ぶことによりグラフが出来ます。ちなみに握手補題の証明は、次のようになります。
1回の握手には2人の出席者が関与するので、出席者が握手した回数の総和は、握手の総回数の2倍になる。したがってそれは偶数になる。
グラフの言葉を使わなくても証明できますが、グラフを見ながら考えると見通しが良くなると思います。
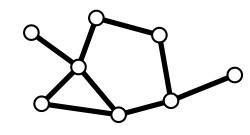
この例のようにグラフで表現することによって、問題の本質部分を浮き上がらせることができ、また図に表されることによって視覚にもうったえ直観的にもわかりやすくすることができるようになります。インターネットや、鉄道網、道路網のように、もともとグラフそのものに見えるものもありますが、上の例のように、人間と人間の関係を表すグラフもあり、潜在的にはいたるところにグラフがあると言えるでしょう。そのようなグラフの様々な性質を調べるのがグラフ理論です。以下では、グラフのマッチングに関する理論の一端を紹介します。
今度のパーティーは合コンです(婚活パーティーと呼ぶのがよいかもしれません)。男女n人ずつが出席しているとします。宴も酣(たけなわ)となったところで、それぞれの出席者に、結婚してもよいと思った異性を、複数回答可で挙げてもらい、お互いにそう思っているペアの中から、なるべくたくさん結婚するペアを作ることを考えます。この問題の場合も、お互いに結婚してもよいと思っているペアを辺で結べば、図2のようなグラフが出来上がります。
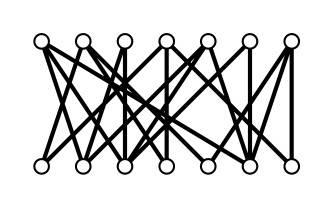

図3に、試しにペアを作ってみました。このような辺の選び方をマッチングと呼びます。男女が1人ずつペアにならずに余っていますが、うまく全員が結婚できるような組合せがあるでしょうか。実は答えはノーです。その理由は図4を見れば一目瞭然です。二重丸になっている4頂点のつながっている先が、併せて3頂点しかありませんので、4人のうちの一人は余ってしまうことになります。
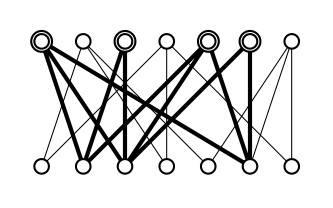
上の二重丸の頂点たちのようなもの、つまり、何人かが自分たちより少ない人数を取り合うと、誰かが結婚できなくなるわけですが、実は、そのような「何人か」がどこにもいなければ全員が結婚できる、ということが知られています。これを結婚定理と呼びます。
マッチングの問題は、一対一でペアを作る、という意味で、結婚になぞらえることが多いですが、仕事などの割り当て問題にも適用されます。数独などのパズルも、どのマスにどの数字を割り当てるか、という部分に焦点を当てるとは、マッチングの問題と捉えることもできます。問題をグラフという構造に抽象化して考えることで、いろいろな分野へ適用できる概念になるわけです。


