数学は人類の歴史と共に始まった、と言えるほどの長い歴史を持つ学問ですが、現在でも非常に活発に研究活動が進み、めざましく発展している科学です。
数学を研究するということは、数学の受験勉強をすることとはまったく違います。数学の研究は山登りにたとえられます。一歩一歩上に登っていくと、あるところで景色が開けて、今まで複雑と思っていたことが、実はこんなふうになっていたのか、とわかるときがあります。高校や大学初年の数学であっても、新しいことを知ってみると、以前に習ったことが見通しよく理解できた、という経験をした人はいると思います。この世界はどうなっているのだろうか、という混沌の世界から、少し上に登ってその世界に秩序があることを発見したときには、確かに「数学は美しい」と思います。ただし、人が登ったことがない山に挑戦する(これが研究ですが)ためには、自分で新しい道具(装備)を工夫するなど苦労が必要です。
私が最近研究しているのは整数論、特に岩澤理論という分野です。これは岩澤健吉先生(プリンストン大学, 1917-1998)によって創られた理論を核として発展している分野で、ワイルスによるあの有名なフェルマー予想(n が 3 以上の整数とき、x^{n}+y^{n}=z^{n} には正の整数解は存在しない)の証明も最終的に岩澤理論で決着がつけられました。現在、世界中で研究されています。
たとえば、楕円曲線とよばれる左のような曲線に有理数解がどのくらいあるのか、ということが、p進ゼータ関数という関数の様子によってわかる、と岩澤理論では予想されています。私は、今まで人が扱えなかった楕円曲線が超特異還元を持つ場合に、新しいアイディアを使って研究しています。
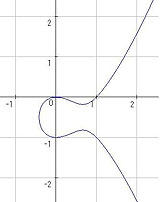
y2+y=x3-x2 の有理数解は (0,0), (1,0), (0,-1), (1,-1) のみですが、
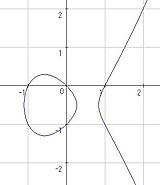
y2+y=x3-xの有理数解は上の4点以外にも (-1,0), (-1,-1), (2,2), (1/4,-5/8), (-5/9,8/27) など無限個あり、この様子はそれぞれのゼータ関数に反映されています。

栗原研でのセミナー風景

熱心に質問をする栗原研の学生


