- Home
- New Kyurizukai
- 4-Dimensional Topology from Keio's Faculty of Science and Technology
4-Dimensional Topology from Keio's Faculty of Science and Technology Understanding 4-dimensional space by focusing on singularities
The key to enjoying mathematics is to let your interests lead you when an intriguing problem presents itself.
According to Hayano, he has had a natural talent for arithmetic and mathematics since childhood. He first learned that math could be a career in his first year of junior high school and set his sights on becoming a mathematician. Wary about whether he would have what it takes to become a full-fledged mathematician, he started full-scale research early on. This led to him earning a Ph.D. in the first year of his doctoral program. We asked him to tell us his secret to sticking with and enjoying mathematics for so long.
Kenta Hayano
Dr. Hayano specializes in low-dimensional topology, mainly studying “4-manifolds” and “singularity theory.” He earned a Ph.D. in Science from the Department of Mathematics, Graduate School of Science, Osaka University in 2013. After teaching as an assistant professor at Hokkaido University, he started working as full-time lecturer in April 2016 at the Department of Mathematics, Faculty of Science and Technology, Keio University. In April 2020, he was promoted to Associate Professor (current position).
The Research
This feature covers Associate Professor Kenta Hayano, who studies figures called “4-manifolds” in the field of topology, a modern branch of mathematics.
“Topology’s front lines,” a highlight of modern geometry
Exploring invisible "4-dimensional manifolds”
The Earth is round. This is now a well-known fact. However, it was not until the 20th century, when rockets were invented, that it became possible to see the entire globe. Currently, we do not have a complete picture of the universe. This is because we cannot observe it from the outside. We may, however, be able to solve this problem through mathematical theory. This is where the field of "topology" comes into play.
What is a “manifold” in topology?
Topology is a branch of geometry. The geometry we learn through high school is called "Euclidean geometry," but topology, a field broached in college-level courses, classifies figures and examines their features in a different way.
Topology deals with figures called “manifolds.” A manifold is defined as “a figure or space in which a part, but not the whole, can be perceived.” The surface of the earth is a "2-dimensional manifold" or “2-manifold” in the topological world. This is because when viewing very small portions of the Earth's surface, it is possible to perceive it as a “flat,” two-dimensional space. It’s easy to think that the surface of the Earth is 3-dimensional since we often depict it using 3D space. However, a better way of phrasing this concept is that the Earth’s surface exists within 3-dimensions. Because we can map the points comprising the surface of a sphere using two independent parameters (x, y), the surface is actually 2-dimensional.
Visualizing unimaginable "4-manifolds”
Topology deals with even higher "n-dimensional manifolds" such as "3-dimensional," "4-dimensional," and "5-dimensional" manifolds. Experts call manifolds with 4 dimensions or less, "low-dimensional manifolds," and those with 5 dimensions or more, "high-dimensional manifolds.”
Among them, Hayano studies 4-dimensional manifolds, more commonly called “4-manifolds.” A 4-dimensional manifold is a manifold in which each of the points that comprise the figure are represented by four independent parameters. Just as there are an infinite number of 2-manifolds, there are an infinite number of 4-manifolds. However, since we can only perceive up to 3-dimensional space, we cannot imagine or physically see what a 4-manifold is.
“Previous studies have developed methods of visualizing the characteristics of 4-manifolds using diagrams. One of them is the ‘Kirby diagram,’” says Hayano.
A Kirby diagram for a 4-manifold looks like what is shown in Figure 1. When you have a specific 4-manifold you’re working with, an important factor in understanding its features is studying singularities of functions defined on the 4-manifold.
“You can work out the shape of a manifold by examining the singularities of a function and other methods. A singularity is the point at which the derivative of the function is zero. A Kirby diagram follows certain rules to capture 4-manifolds by illustrating the positional relationships between the singularities of their functions,” Hayano explains. He posits that while the average person is incapable of picturing the shape of a 4-dimensional manifold, topologists can by simply looking at a Kirby diagram. It’s worth noting that there are other methods to use diagrams to visualize the features of 4-manifolds. For example, Figure 2 illustrates the "trisection" technique, in which the location of singularities of a function on a single 4-manifold is represented by three schematic diagrams.
Hayano says that he studies various 4-manifolds and discusses their characteristics with his students on a daily basis.
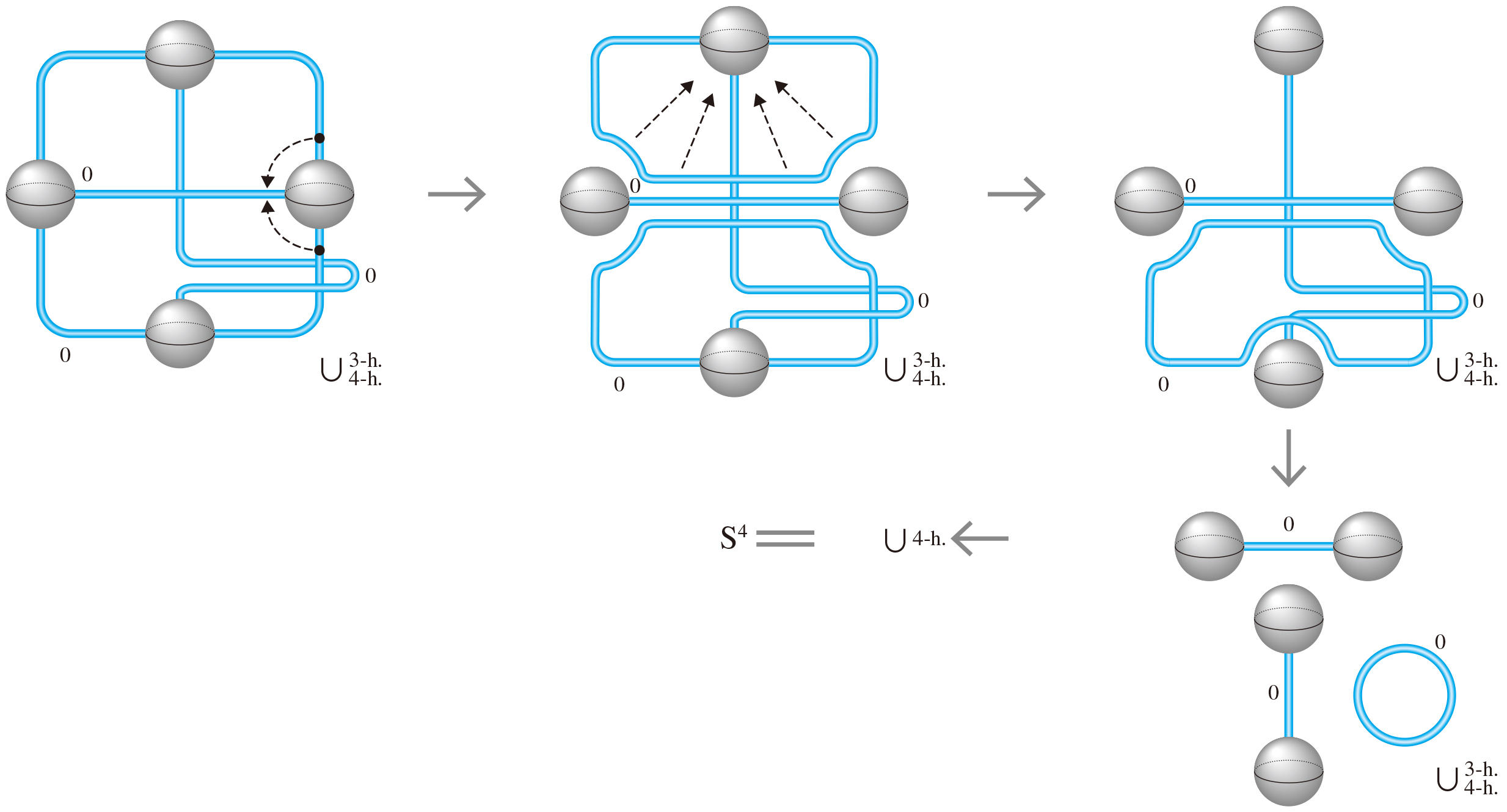
Fig.1 Deformation of a 4-manifold
A deformation of a 4-manifold using a Kirby diagram for a paper Hayano presented during the first year of his master's program. It shows a 4-dimensional manifold (left), when deformed using the Kirby scheme, proceeding as the arrow indicates, eventually arriving at the "4-dimensional sphere" (bottom right), the simplest of all 4-manifolds.

Fig.2 Illustrating the figure of a 4-dimensional manifold
In a technique known as “trisection,” the position of singularities of a function on a 4-dimensional manifold is shown using three figures.
4-manifolds; a major development in the “gauge theory” of quantum mechanics
“I was very interested in the fact that with 4-manifolds, there is a big difference between 'topological structure' and 'differential structure,'" says Hayano.
“A topological structure is a structure defined solely by the way each point in the manifold is connected. On the other hand, differential structure, which looks at the form’s ‘smoothness’ to classify manifolds in further detail. Differential structure is a type of topological structure that contains more information about the shape of the manifold," he explains.
In Euclidean geometry, which students learn up through high school, figures are classified according to the lengths and angles of their sides. In the field of topology, Hayano describes how he is "motivated to come up with structures for manifolds that posit additional information, much like differential structure, and further classify them accordingly."
“In the world of topology, people say that with 2-manifolds 'A cup of coffee and a doughnut are the same thing.' Both have a single hole, and when deformed (flattened) they become the same shape. This classification is based on the topological structure of the manifold that focuses on the how the points that make up the figure are connected. Unfortunately, the difference between topological structure and differential structure does not appear in manifolds with 3 or fewer dimensions, so humans cannot really experience it, but in 4-manifolds, the difference between topological structure and differential structure is remarkable," Hayano explains.
He is also interested in the "complex structure" of 4-manifolds. “If a manifold has a complex structure, it will have both topological and differential structure. The opposite is not always true. Just because a manifold has topological structure does not mean it has differential structure, and just because it has differential structure does not mean it has complex structure. Among 4-dimensional manifolds, two can share the same topological structure but have different differential structures. You can also have two differential structures for the same manifold, with one obtained from complex structure but not the other. It’s these types of details that really attract me to researching 4-manifolds,” Hayano explains.
The existence of 4-dimensional manifolds that have topological structure but lack differential structure comes from the Rokhlin's theorem, which was proved in 1952. It was again proven in 1982 by British mathematician Simon Donaldson (1957-present), who used the gauge theory of quantum mechanics to demonstrate that 4-manifolds with multiple different differential structures exist. This led to major developments in the study of 4-dimensional manifolds.
Will we ever know the "shape” of the universe?
You may be wondering what the point of studying n-dimensional manifolds is.
According to Hayano, “You can't untangle two intersecting lines on a flat, 2-dimensional plane. However, when expanded to 3-dimensional space, the two lines can be distinguished when crossing below or above the other, making it easy to understand the intersection. As you increase in dimension, you have more freedom to move the manifold, which makes it easier to perform operations such as untangling intersections, therefore making the manifold easier to work with.”
In fact, cutting-edge physics research hypothesizes that "higher-dimensional spaces” exist beyond the 4th dimension while string theory suggests that the universe may be 10-dimensional if the dimension of time is included. Therefore, topology, which deals with higher dimensions, has become an important mode of research.
It may not be long before Hayano and other topologists are able to solve the mystery of the shape of the universe.
(Interview and text writer: Kumi Yamada)
Interview
Associate Professor Kenta Hayano
Learning about math as a career through TV dramas
What made you decide to become a mathematician?
When I was in the first year of junior high school, I watched the TV drama "Yamato Nadeshiko" which is how I learned that you could do math as a profession. I started to think seriously about becoming a mathematician when I entered high school, and decided I would major in mathematics when I got to university. That being said, I did more than just study math in high school. I was also crazy about swimming and spent my summers swimming more than 10 kilometers a day at camp. I was born and raised in Osaka and, as I’d hoped, I got into the mathematics department at Osaka University which I could commute to from my home.
Among the areas of mathematics, what made you choose topology?
Actually, I didn’t study much during the first two years of my undergraduate program. Instead, I joined a competitive student dance club and spent my all my time practicing for that. I chose it because I thought the club members looked like they were enjoying themselves when I saw them at a recruitment event for freshmen. Competitive dancing turned out to be really fun! I was completely hooked. But that feeling gave way to anxiety in my junior year when I realized I needed to get serious about math. I quit my extracurriculars and started focusing on my studies. Just around that time, I decided to attend a small mathematics seminar that was starting on campus. The seminar teacher recommended I read a book on topology. The more I read, the more intrigued I became. By the end of my junior year, I had made up my mind; I was going to join the topology lab in my senior year.
I heard that you went on to attend graduate school at Osaka University and even studied in Germany.
I started writing my paper in the first year of my master's program. Right around that time, I learned of a professor who had published a paper dealing with the same topic as mine. Despite researching the same subject, some of our results were different, so I asked my advisor to contact them so we could meet. After our meeting, the co-author of that person’s paper invited me to Germany to study at the Max Planck Institute for Mathematics for six months while I was a doctoral student. This was my start with joint research. It was an incredibly valuable experience that was possible because I had the luxury of time, being a grad student at the time. I consider myself very lucky.
Starting research early to test his mettle as a mathematician
In your first year as a doctoral student, you were both selected as a Research Fellow of the Japan Society for the Promotion of Science (JSPS) and received your doctoral degree in one year. Does that mean you started working on your dissertation before your program began?
Trying to become a mathematician is a risky move. I was quite anxious as a junior and senior in university when contemplating whether I could support myself in the future if I pursued math as my career. My professors often stressed that study skills and research skills are two different things.
I was confident in my ability to study and learn material as long as I was given time, but I couldn’t gauge my aptitude for research. So, I decided to begin research early on to see if I had what it takes to make it as mathematician. From the second half of my senior year, I began to approach my studies with research in mind. By the first year of my master’s program, I started a full-fledged research project. There are many different fields within mathematics. I was careful to avoid those that would take a considerable amount of time to study before I could begin writing my thesis. It’s a moot point now, but if I hadn’t chosen to become a mathematician, I was considering working for an insurance company as an actuary.
After completing your doctoral program, you taught at Hokkaido University?

I was offered the job after applying for an open position. Hokkaido was great. The food was delicious, and it was perfect for winter sports. The position had a maximum term of 5 years, so rather than waiting for my contract to run out, I took up another open position at Keio University in 2016.
The demand for people with a background in mathematics in the business world
What path do most math majors take after graduation?
Many of them go on to the corporate world or end up becoming math teachers at middle schools and high schools. However, as far as my field is concerned, I’m confident saying that there are almost no companies looking to hire an expert in topology [laughs]. There are some niche opportunities, though. I am currently collaborating with a researcher at a gaming company who is working on automating the development of game software through artificial intelligence (AI) using “singularity theory,” which is also central to the study of 4-manifolds. Machine learning and deep learning with AI are currently being used in many fields, and I feel that there are quite a few areas where singularity theory could prove useful. According to my contact at the gaming company, “people with an academic background in mathematics are in high demand. Anyone can learn some basic programming skills. The ability to understand the program from a more wholistic perspective, though, cannot be acquired overnight. People who have studied mathematics have that ability."
Understandably, it may be difficult to picture viable career paths when it comes to mathematics, but students shouldn’t have any trouble finding a job. In fact, it seems that more and more companies are saying, “We want to hire people with a Ph.D. in mathematics.” Today, there are few companies that have yet to adopt IT. People with a background in mathematics are in great demand across a variety of industries.
Is there anything you keep in mind when teaching Keio University students?
When conducting research, it is important to exercise your brain and think things through. In our daily seminars, we try to encourage students to think carefully and come up with solutions by themselves. I may give some hints, but I try my best not to give out the answers.
Prioritizing the “fun” of mathematics
What advice would you give to high school students who want to major in mathematics in university?
First of all, anyone who is willing to learn is welcome. Unlike chemistry or biology, mathematics requires no laboratory equipment or chemicals, costs very little, and can be started at any time. Most high school students probably think of mathematics as only “solving problems,” but this is not the case. It is much more important to understand what is written in textbooks and reference books than to solve problems. As such, I hope that students will develop the ability to focus and read textbooks early on. I also want them to be able to identify areas they find interesting and think through these subjects on their own.
Furthermore, I hope that they come to appreciate the definitions of the technical terms they encounter when studying mathematics. For example, in high school, students learn about "local maxima and local minima.” Problems such as finding the value of a local minimum point (local minima) can be solved by differentiating a given function. Even knowing this, few students can provide a correct answer when asked to explain what the term “local minima” means. If you don’t actually understand what “local minima” means, you will end up with a superficial knowledge of computation at best. If mathematics were simply a matter of crunching numbers to find answers, then we would leave it to computers nowadays. It isn’t just about finding the answer—it is far more important to understand the meaning behind the answer. This is why I encourage my students to go deeper when learning terminology. This is applicable not only for mathematics, but for all natural science disciplines.
What are your future goals as a mathematician and what are your dreams for the future?

I currently have several unsolved problems that I have been working on for the past 3-4 years. Of course, solving them would be amazing, but I would be perfectly happy if I could simply continue working on them every day. I never push myself to the point of anxiety or compromise my physical wellbeing over not being able to solve a particular problem. The key to enjoying mathematics is letting your interest guide you to the problems you work on. I don’t harbor any secret ambitions or get myself worked up saying things like “I WILL solve X problem in my career if it’s the last thing I do!” [laughs]. I would like to keep the focus on having fun while working in mathematics.
Some words from Students…
In my Junior year, I became fascinated with topology after sitting in on one of Dr. Hayano's lectures. He really had a way of explaining concepts that’s easy to understand. I wanted to go more in-depth with topology, so I chose his lab for my research project. His attentiveness in the classroom carries over to his lab. Thanks to his guidance, I can feel myself making steady progress and building up my understanding of the subject matter.
I also appreciate the fact that, although there are many wonderful professors in the Department of Mathematics, Professor Hayano is on the younger side, friendly, and is very easy to talk to. I plan to get a corporate job after completing my master's program. I doubt my research on topology will be directly applicable in the workplace, but I believe that the logical thinking skills I have acquired through mathematics can be used in any profession. (1st-year master's student)


