- Home
- New Kyurizukai
- Adaptive Algorithm
from Keio's Faculty of Science and Technology
Adaptive Algorithm
from Keio's Faculty of Science and Technology
Pursuit of an ultimate filter
that extracts desired information from signals
It’s interesting to persistently pursue apparently minor things that are less popular among most other people.
Over the years Dr. Yukawa has taken up and persistently pursued hobbies and sports, such as soroban (abacus, a traditional calculation tool), table tennis and dancesport, which appear to be minor (in Japan) yet are of great depth. This attitude overlaps with his mindset as a researcher who devotes himself to the theoretical side of studies rather than jumping at themes in fashion. Behind his way of life were valuable encounters with good friends and respected teachers, not to mention the support from his family.
Masahiro Yukawa
Dr. Yukawa received the B.E., M.E., and Ph.D. degrees from Tokyo Institute of Technology in 2002, 2004, and 2006, respectively. He is currently an Associate Professor at EEE Department of Keio University. He is pursuing a new horizon in the field of Signal Processing using mathematical tools, particularly Convex Optimization and Fixed-point Approximation. He has served as an Associate Editor of several journals including IEEE Transactions on Signal Processing. His academic carrier includes Postdoctoral Fellow at University of York, U.K. (JSPS Postdoctoral Research Fellow); Special Postdoctoral Researcher at RIKEN; Guest Researcher at Technische Universität München, Germany; and Associate Professor at EEE Department of Niigata University. He received the Young Scientists' Prize, the Commendation for Science and Technology by the Minister of Education, Culture, Sports, Science and Technology in 2014, among many others.
The Research
Associate Professor Masahiro Yukawa featured in this issue, whose field of research focuses on an ultimate adaptive filter capable of freely extracting desired information from signals.
What is an adaptive filter that extracts and elucidates useful information from signals?
Dedicated to creating an “ultimate filter” to unravel highly complex phenomena
Our society is brimming with truly diverse signals (information), such as visual images, sounds, radio waves, brain waves and stock price fluctuations, to name a few. The primary role of signal processing is to convert these signals into numerical form and extract only a desired piece of information for identifying the characteristics of a given phenomenon or using it to make a projection. By taking a mathematical approach and making complex signals obtained from diverse phenomena in the universe easily usable, Associate Professor Masahiro Yukawa is intent on establishing a mathematical system useful for extracting needed information.
Signal processing – the backbone of electronics industry
“Suppose our modern world loses signal processing, we will suddenly find our life totally inconvenient and boring – no TVs, no mobile phones, no digital cameras and no airplanes flying in the sky. MRI, the medical equipment, is also a product of signal processing. Popular topics of our conversation of late, such as drones, androids and big data analysis, are also impossible without signal processing. In short, signal processing is something essential to our modern life just like air,” mentions Dr. Yukawa.
For example, the microphone converts cellular phone sound into and the image sensor converts images captured by a digital camera into electrical signals, respectively. By replacing these electrical signals with numeric sequences, they come to be mathematically processed and become objects of the so-called signal processing.
“What I have actually focused my effort on is adaptive processing of acoustic and radio communication signals. One example is the echo canceler. In videoconference or cell-phone conversations, your voice may echo back to yourself belatedly via the other side’s microphone, which is often annoying. The echo canceler is designed to cut the echoed voice only. Because your echoed voice is not necessary, signal processing performs subtraction and allows only the other side’s voice to be delivered. Likewise, in the case of radio communication, adaptive signal processing deals with multiple communication data, which simultaneously arrive in the base station, separate and deliver them to individual users. What is indispensable to such signal processing is the “adaptive filter.”
The role of adaptive filter is to estimate a function from data
Just like a coffee filter, the adaptive filter extracts, through a mathematical operation called “filtering”, an exactly needed piece of information.
“Speaking of sounds, the role of the adaptive filter is to estimate the function f capable of extracting the required sound x from the observed sounds y. Putting it another way, we simply have to seek the function f because we need to estimate x from y,” explains Dr. Yukawa.
As the term “adaptive” suggests, however, we, operators, must work – flexibly adapting the filter function to the constantly changing environments. In other words, the adaptive filter’s performance depends largely on our ability to express, in real time, a function made as closer as p ossible to the required information while minimizing computational complexity.
Here’s a major problem: most of actual phenomena are of nonlinearity, which is difficult in general to be handled mathematically. Nonlinearity means not being linear. In short, with these phenomena, input and output are not proportional to each other. Attempting to deal with nonlinear data causes the amount of computation to suddenly increase, making it difficult to extract the needed information speedily.
“Volterra filter and neural network are typical approaches to handling nonlinear data. But the former involves enormous volumes of computation while the latter has the drawback of ending up with a local minimum. To address these problems, I decided to adopt what is known as the “kernel adaptive filter” based on the kernel method.
The kernel method allows data to be mapped onto a feature space of higher dimensions (for example, from two dimensions to three dimensions), thereby converting a group of data into an easierto-handle group. This technique is widely used for facial recognition and other pattern recognition as well as big data analysis. Formerly it was used in batch processing, a method to process batches of collected data all at once. In recent times, it is increasingly in use for online scenarios in which new data are collected and processed from moment to moment.
“ I would omitexplanation of reproducing kernel because it is too technical and difficult. But the benefit of reproducing kernel exists in that it can evaluate a function value as an “inner product.” A simple example of an inner product is the sum of all products that have been obtained by multiplying two vector elements in series. The inner product makes it possible to express correlations between two vectors. Once these correlations can be expressed with an inner product, we can now use our knowledge of linear models to the fullest,” Dr. Yukawa states emphatically.
In short, you can say that the greatest advantage of this method is that it allows us to use the easy-to-compute linear theory in dealing with usually difficultto-handle nonlinear data.
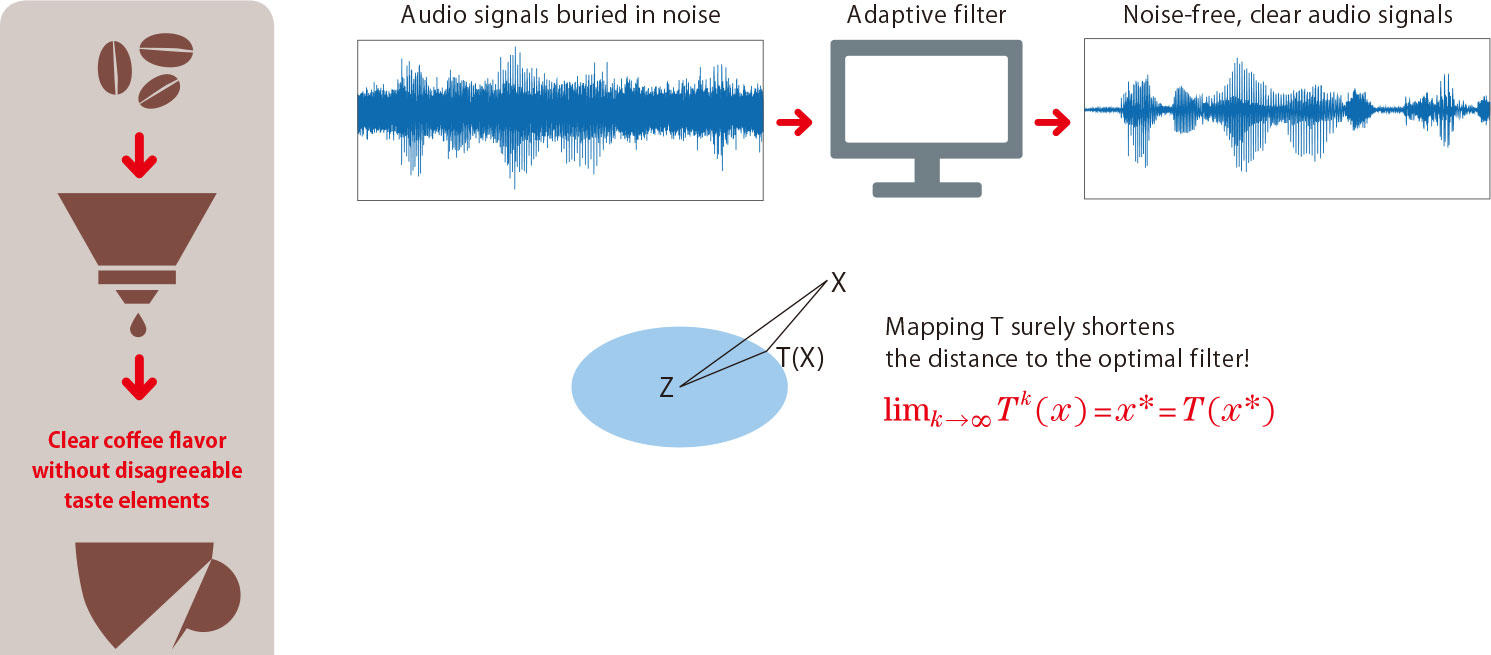
Fig. 1 Adaptive filter: its application example and basic principle
Functioning like a coffee filter for removing disagreeable taste elements from coffee, the adaptive filter can be used to extract clear audio signals by removing noises. The basic algorithm for updating a filter coefficient is based on a kind of nonexpansive mapping known as metric projection. When mapping T is a weighted average of a “nonexpansive mapping with fixed points” and the “identity mapping,” it is known that the filter converges to a fixed point x* as T is operated repeatedly (Mann fixed-point theorem).
Extracting exactly needed information in real time
Dr. Yukawa has developed the “multikernel adaptive filter,” based on the kernel adaptive filter and making the most of the latest developments in convex optimization.
“To put it in a general image, the filter I developed approximates a function’s waveform by adding up bell-shaped curves known as Gaussian kernels. We prepare in advance a number of Gaussian kernels – wide and low curves, narrow and high curves, etc. – then arrange coefficients, which determine their heights, in matrices. Finally, we estimate the function by adding up a smaller number of peaks.”
“The key point here is to include a mechanism designed to automatically identify peaks that fit the function you wish to estimate while nullifying coefficients for most of the other peaks. Sparse matrices refer to those matrices that contain many zeros. Neat arrangement of information (in sparse matrices) enables optimal model selection.”
This allowed us to adjust Gaussian kernel widths to nonlinear function forms adaptively and automatically and respond freely to function forms even when they may change with a lapse of time. Highly accurate estimate is thus possible with a smaller number of peaks.
“By using this technique, for example, we can make highly accurate, real-time predictions of future power outputs in solar power generation on the basis of power output data of the past,” he adds. The “fixed-point theory for nonexpansive mapping” is the mathematical foundation for Dr. Yukawa’s study.
“A fixed point refers to a point that does not move even when mapping T is operated, that is, x such that Tx = x. Also, nonexpansivity refers to the characteristic which the operation of a mapping does not expand the distance between two points. Today, it is becoming increasingly known that solutions to problems – in various fields of science and engineering – can be expressed as fixed points of a mapping. Actually, the use of a nonexpansive mapping makes it easy to design fixed points, or algorithms to seek the solution of a problem. The multikernel adaptive filter estimates unknown functions by expressing everchanging functions as fixed points of a mapping which is created using data that flow in from moment to moment,” he remarks.
Dr. Yukawa expresses his desire to create an “ultimate filter” in the future – the ultimate filter capable of dealing with any complex phenomena. After 2015 set in, Dr. Yukawa is making a name for himself internationally as three of his papers were already accepted for publication in the journals of IEEE (The Institute of Electrical and Electronics Engineers, Inc.) and he was picked out as an Associate Editor for the world premium journal in the field of signal processing. He continues to focus on fundamental mathematical systems underlying the currently highlighted research themes such as distributed signal processing, big data analysis and deep learning while taking a side glance at them.
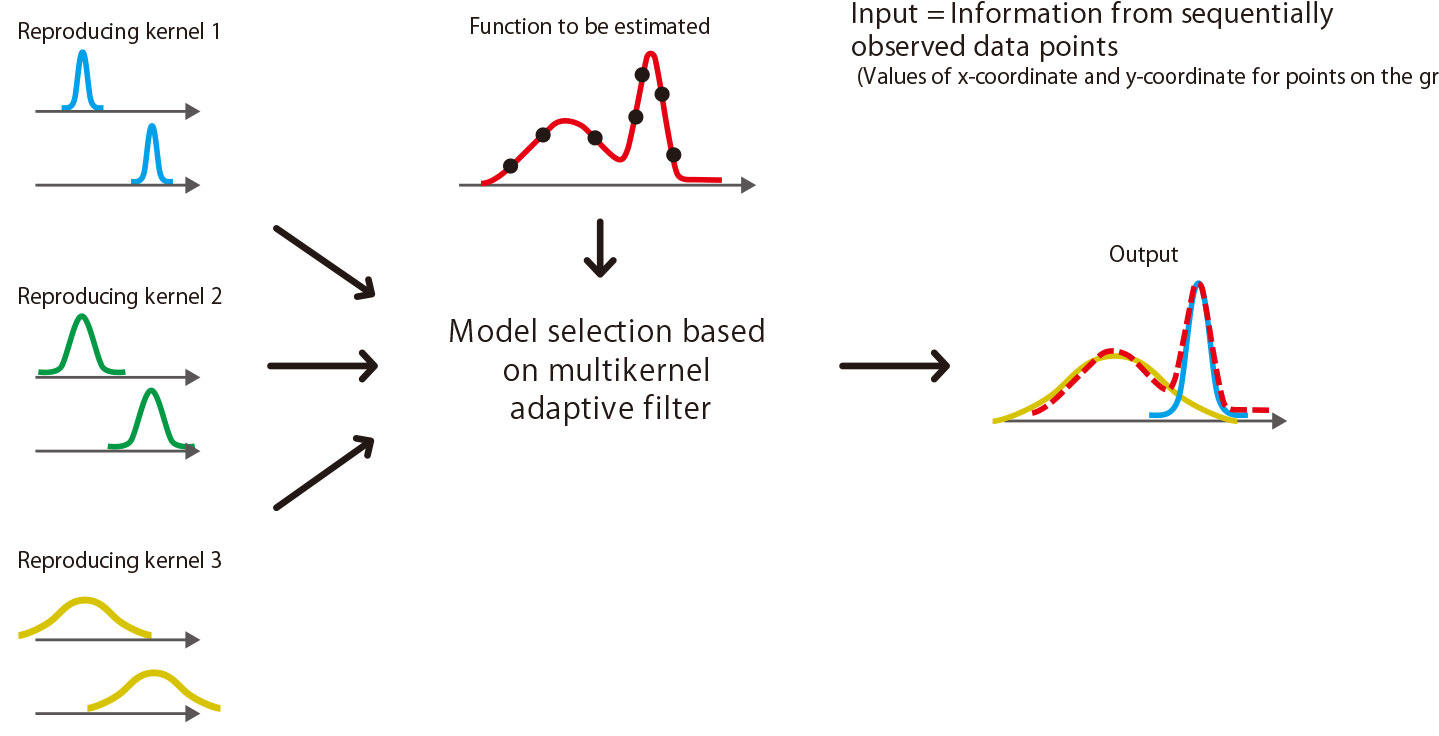
Fig. 2 Model selection conceptual diagram based on multikernel adaptive filter
By using information from sequentially observed data points and allowing the filter to learn through an adaptive algorithm, it is possible to automatically select mathematical models (reproducing kernels) that can adequately express local structures of the function you wish to estimate. The adaptive algorithm incorporates knowledge from “sparse representation” and “fixed-point theory of nonexpansive mapping.”
Interview
Associate Professor Masahiro Yukawa
Being good at mental calculation and arithmetic since childhood, I gradually came to have an interest in mathematics.
What was your childhood like?
As far as I was told by my mother, I was a very talkative boy, who often reported to my nursery school teacher about everything that had happened at home the day before. To make the matter worse, I spoke out clearly and in an easy-to-understand way. Later my mother complained to me that she had felt pretty embarrassed (Laughter).
I have a sister four years older than me. As a small boy, I used to follow her and play house with her. This gave me a nickname “shadow-like follower” (Laughter).
I was born in Minami-Ashigara City, Kanagawa Prefecture. Both my father and mother were public servants, father working for the Odawara City Office and mother for the Ministry of Finance’s Printing Bureau. Both of my parents were good at math in their school days. Presumably having inherited their genes, they say I was good at mental calculation since my nursery school days. But I have few memories of those days. The only thing I still member is that, as an elementary school boy, I often went shopping with my mother, when I did sums in my head.
Because of my mathematical interest, I was very fond of riddles, quizzes and puzzles and loved reading books about mathematics.
Soon after entering the elementary school, I attended a soroban school. Thanks to a good teacher, I liked the art of soroban and continued to learn it up to the end of junior high school second year. I hold a first dan license in soroban and a third dan license in mental calculation. On the occasions of soroban competitions, I was always among the best; at an All Kanagawa Prefectural soroban competition when I was an elementary school sixth grader, I became the champion in the category of calculating figures read off aloud. Even today I still do two-digit addition and multiplication by mental calculation – not so well as in the past, though.
I used to teach arithmetic and mathematics to my friends. Looking back now, I may also have learned something by teaching them. I’m still grateful to my friends.
Were you an indoor-oriented boy?
I don’t think so. An expanse of rice fields could be found around my house, so rice and flower fields were ideal playgrounds for us children. Actually I was an active elementary school boy; the moment recess time began, I dashed out of the classroom into the schoolyard to enjoy ball playing with classmates. There was also a period when I went to school at 6:00 in the morning just to practice long-distance running together with my friends – a cherished memory now.In my junior high school days, I served as captain of the table tennis club and even participated in the prefectural tournament. The more I exercised, the better I slept at night (Laughter).
Meanwhile, at one time I was crazy about “Famicon” video game machine and “Game Boy” handheld game device. I played and played these games until I got sick of them. Having done too much, I said good-bye to these games (Laughter).
Didn’t your parents tell you to study hard?
No, they didn’t. My parents never criticized me about my attitude about studies because I did at least what I should do – I did homework as assigned and listened carefully to classroom lessons. I’m grateful to my parents for basically allowing me to do whatever I liked. When I was an elementary schoolboy, I was making a plastic model and badly soiled the carpet surface here and there with a sticky bond. Even at that time I remember they didn’t scold me at all. As parents they must have been very generous.
Following entry to a local junior high school, I began to attend a small cram school in my neighborhood partly because of my elder sister’s influence. Thanks to the cram school teacher’s enthusiastic guidance, I became more and more interested in mathematics. In those days, however, I wanted to become a certified public accountant in the future, not a researcher.
As for senior high school, I chose Prefectural Atsugi High School, which was outside of my school district. It was my routine to make a 40-minute trip one way on the Odakyu Line train while reading the mathematics textbook on board. Presumably, this experience may have made my backbone as a researcher as I am today.

From halfway through the first year to the end of the second year, one of my schoolmates and I took up a part-time job at a co-op store near my high school – for a bit of real-world experience and earning pocket money. There I was assigned to the deli corner, so it became my special skill to neatly wrap food in cellophane. Once I demonstrated this skill and surprised my wife (Laughter).
After all, I spent most of the money I earned from this part-time job for music, buying an acoustic guitar and so on. I liked to chant numbers from “SPITZ” (a Japanese rock band) and other J-Pop artists to my own accompaniment, but I was too shy to appear in front of an audience … (Laughter).
As a high school third grader, I began to think seriously about the university entrance exam and began attending a prep school aiming to enter the engineering course. On the occasion of the school’s autumn cultural festival, all of us classmates were excited to bring our dancing performance and other programs to success. It seems to me that the extraordinary energy I exhibited during the festival somehow fueled my last spurt for the university entrance exam.
As an undergraduate I focused on dancesport and part-time jobs.
You advanced to the 5th Academic Group of Tokyo Institute of Technology, didn’t you?
I did so partly because of recommendation by a father of my friend and partly because of advice by a tutor at my prep school. By this time, I became inclined, vaguely though, to choose in the future a career based on IT-related or mathematical knowledge.
To be honest, however, I was not so serious about study while I was in the lower undergraduate grades. Although I knew I was interested in theory-oriented subjects, such as on Fourier transform and Laplace transform, I was still unable to narrow down my academic interest. Under such circumstances, as an undergraduate I focused on club activities and a part-time job at a fast food restaurant. The fast food restaurant provided me with an opportunity to interact with students from other universities; for me working there was as enjoyable as a club activity at university.
Another pursuit I took up after entering the university was dancesport. While inspired by a TV program as the first opportunity, I can say that something minor, or something that not many people are doing, caught my interest. The dancesport club had only four or so male members for each undergraduate grade – really minor wasn’t it (Laughter)? In this sense, it seems to have something in common with soroban and table tennis. Turning to my research side, signal processing is quite popular in the world, but I’m focusing on themes on which few people have an eye on.
My specialty in dancesport was Latin dance. I continued this pursuit for about ten years. Some jokingly say that I chose England as my study-abroad destination because it is the home of dancesport. The fact is that in England I participated every week in a more elegant ballroom dancing practice session, not dancesport … Meanwhile, I went to watch dancing competitions from time to time and I was particularly get excited when I visited Blackpool, which is the place of the Blackpool Dance Festival, to watch an amateur competition. At the time, the TV show “Strictly Come Dancing” was winning great popularity among British viewers.
It’s a surprise. Were you not shy when dancing with a female partner (Laughter)?
In the beginning yes, but very soon I got accustomed to dancing with a female partner. To tell the truth, soon after marriage I invited my wife to enjoy ballroom dancing with me, but she gave up after only several times. Her excuse was that she got fed up with the way I instructed, which was too strict and specific … (Laughter). I didn’t mean to be too strict with her, but it seems that the habits I had acquired through dancesport lingered, which urged me to specifically advise her on posture, shift in the center of gravity and so on. In everything, once I get started, I tend to forget myself, which, I admit, is my forte as well as my shortcoming.
It was when I became a senior and joined a lab specializing in signal processing and communication theory that I became hooked on the attraction of research work. The lab I initially had in mind was one focusing on computer vision, but the number of applicants was more than the capacity the lab could accommodate. Playing “rock paper scissors" was the only way to decide new members, so I gave up the game and switched my wish. Looking back now, this change to the theory-oriented lab proved to be the right answer.

Studying in the master program, I came to have opportunities to present my research works at international conferences, which motivated me to study more and more – so immersed in study that my desire to live a researcher’s career became immovable and I made up my mind to advance to the doctoral course. Halfway through the doctoral course, I was adopted as a research fellow of the Japan Society for the Promotion of Science, which allowed me to study while receiving salaries and research funds.
Although it was already decided that the Institute of Physical and Chemical Research (RIKEN) would employ me as a Special Postdoctoral Researcher – a coveted post – following completion of the doctoral course, I was fortunately able to complete the course six months earlier. Taking advantage of the remaining six months, I visited the U.K. to study at University of York. After returning from the U.K., I worked at RIKEN for about three years from April 2007, engaging in research into mobile communications and adaptive filters. During my period with RIKEN, I also had the opportunity to study at Technische Universität München (TUM) in Germany for a brief period of four months.
Then I worked for Niigata University (April 2010 ~ March 2013) before accepting a post at Keio University.
Encounters with good teachers paved the way for my researcher's career.
Sounds like you have smoothly proceeded with your research career.

So far, so good. I’m sure the fact that I have somehow been able to continue research work to date owes much to valuable encounters with good teachers and advisers at each turning point of my life. Above all, my special gratitude goes to Prof. Isao Yamada at Tokyo Institute of Technology and Dr. Shun-ichi Amari at RIKEN, not to mention the soroban instructor and the prep school tutor in my younger days.
By way of repaying my obligations to these teachers, I’m trying to teach and guide my own students as earnestly as possible. But I’m afraid my eagerness may sometimes be too much for them (Laughter). When dealing with my son, meanwhile, I’m trying not to be too particular about his studies just as my parents did for me.
How do you take a breather from your busy research work?
Ever since my childhood, I like eating; so each meal is the best breather for me. Next, my blissful time is when I listen to jazz or Latin music while enjoying sweets together with a cup of coffee that I’ve brewed for myself. My routine on the campus is to go to the cafeteria together with my students. I also enjoy a coffee break with them, which is enjoyable.
What do you think are good points of Keio University?
Keio has a well-developed public relations system effectively encouraging us younger researchers in research activities, for which I’m truly grateful. At Keio, even lower-grade students have easy access to professors – or an easy distance between students and professors, you might say. This is an enviable environment. Keio also offers a variety of student support systems, allowing them to become conscious of their future courses at an early stage. This is another strong point of Keio.
Some words from students
Student : Dr. Yukawa has a cool, objective eye to research, yet demonstrates extreme enthusiasm when striving to achieve research goals. His pet phrase is: “Let’s make our lab No. 1 in the world!” Our lab is a pleasant place to be in, always brimming with conversations and laughter – exchanging ideas and developing discussions during lunch meetings or coffee breaks.
(Reporter & text writer: Madoka Tainaka)


