- Home
- New Kyurizukai
- Arithmetic Geometry
from Keio's Faculty of Science and Technology
Arithmetic Geometry
from Keio's Faculty of Science and Technology
Approaching problems in number
theory using geometric intuition
Expanding the world of mathematics Connecting different fields through abstraction
Kenichi Bannai in interested in solving problems in number theory using a geometric approach. He spent most of his childhood in the United States before permanently returning to Japan in high school. It was during this period that he became increasingly fascinated by mathematics. He loves mathematical speculation so much that it has now become his major “hobby.” Bannai has found in mathematics the capacity that could guide our relationships with society or with other members of community. Based on this experience, he aims to promote mathematics in a more open way.
Kenichi Bannai
Kenichi Bannai is a researcher in arithmetic geometry, a field of mathematics which uses geometric intuition to solve problems in number theory. Using arithmetic geometric objects such as the polylogarithm, he has been studying the relation between abstract arithmetic geometric objects and special functions, with an eye towards solving conjectures concerning special values of L-functions. He received his doctoral degree in 2000 at the Graduate School of Mathematical Sciences, the University of Tokyo. The following year, he became an Assistant Professor at the Graduate School of Mathematics, Nagoya University. He visited the École Normale Supérieure in Paris from 2005 to 2007 as a JSPS Postdoctoral Fellow. In 2008, he joined the Faculty of Science and Technology at Keio University. He was promoted to associate professor in 2012.
Introducing Researchers
Featured in this issue is Associate Professor Kenichi Bannai, a researcher in arithmetic geometry – a field of mathematics – tackling unsolved problems in number theory via an approach based on geometry.
Bringing new insight to mathematical conjectures
Balance between logic and intuition
The combination of logic and intuition is a powerful tool in solving many problems. Arithmetic geometry is a field which uses geometric intuition to solve problems in number theory – intuition which may come to you, for example, when you look at geometric figures comprising of points, lines, etc. We paid a visit to Associate Professor Bannai, who is researching problems in number theory – related to properties of integers – using methods of arithmetic geometric.
A delicate balance between
logic and intuition
“When trying to solve a problem in geometry, one may have had the experience of being able to solve it easily by drawing an additional line in the original figure – an approach which stimulates intuition. Arithmetic geometry appro a c h e s pro b l e m s i n nu m b e r theory using concepts of geometry as represented by such figures,” Dr. Bannai outlined his field of study.
What do we mean by geometry? Let’s take for the example the problem of finding all the rational number solutions of the equation: x² + y² = 1. You may of course solve this problem by manipulating the equation. On the other hand, the solution becomes much easier to understand if you think of the equation as describing a unit circle with a radius 1 on a plane (see Fig. 1). (x, y) = (-1, 0) is a rational number solution of this equation. Consider a straight line passing through the point (-1, 0); this line meets the unit circle only at one more point other than (-1, 0). If the slope of this line is a rational number, then the point of intersection provides a rational number solution of the equation. Conversely, if a rational number solution of the equation is given, then if we connect this point to (-1,0), then we obtain a line through (-1, 0) with rational slope. This implies that the rational number solution to the original equation corresponds one to one to the lines through (-1,0) whose slope is a rational number.
Arithmetic geometry, being useful in solving number theoretical problems, has developed alongside number theory. Number theory has a very long history. Even a simple problem concerning integers in many cases has behind it highly sophisticated mathematical theory. Number theory also has many realword applications; it has been applied to cryptography and authentication technology. As an approach to solving problems in number theory, arithmetic geometry is expected to contribute to solving many problems. In fact, the methods were used to prove Fermat’s last theorem and Mordell’s conjecture(*1) .
“What I’ve pursued so far in my research are arithmetic geometric functions known as the polylogarithm. The polylogarithm is related to many important invariants in number theory. There are certain conjectures in number theory that predicts the relationship b e t we e n t wo nu mb e r t h e ore t i c a l invariants which a priori do not appear to be related to each other. If we can present a higher mathematical concept that can explain both invariants in a unified manner, it will help us get one step closer to shedding light on their relationship. The polylogarithm can serve as a useful bridge between them,” remarks Dr. Bannai.
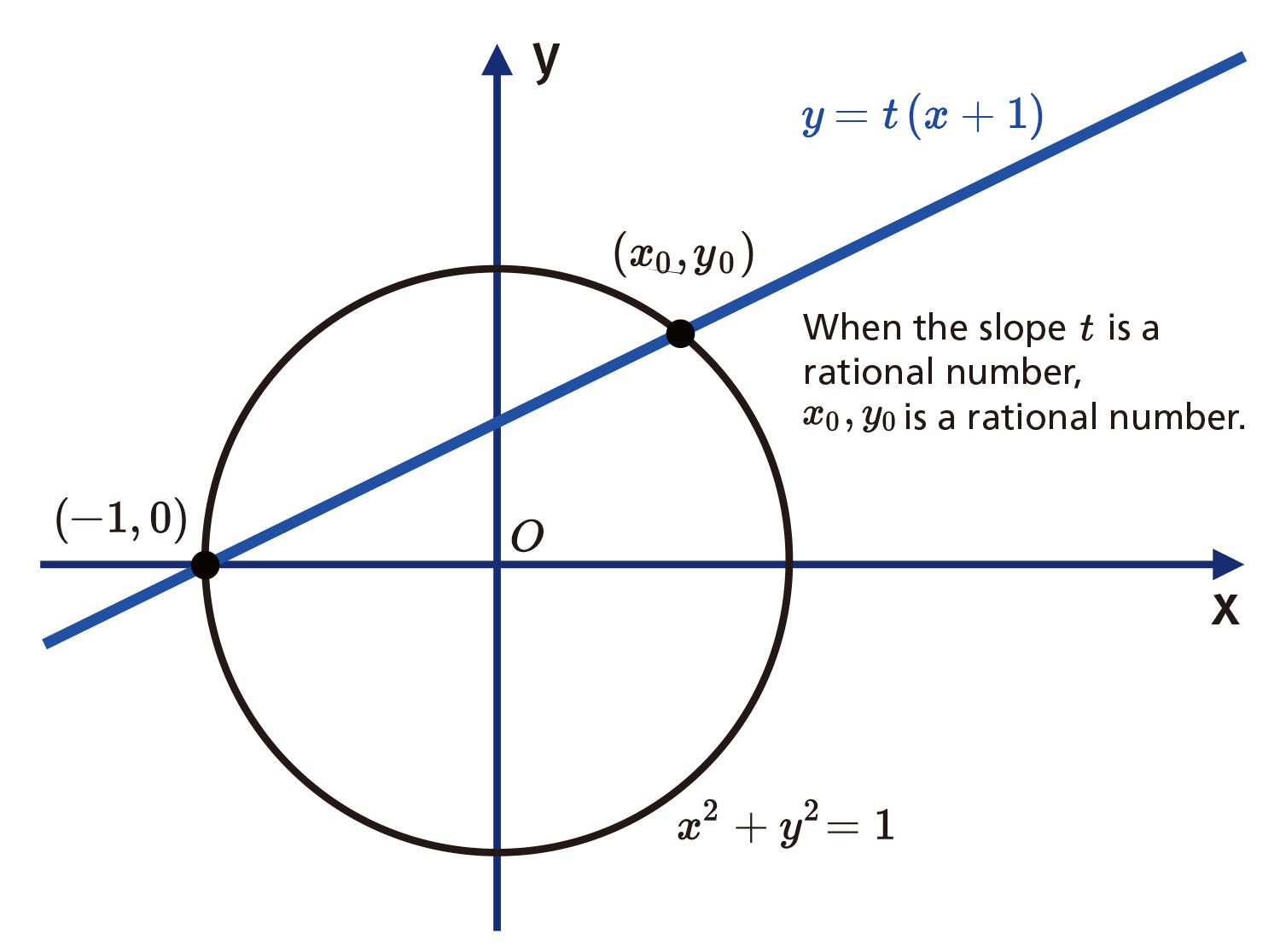
Fig.1 Solving problems in number theory using geometry
A rational number solution for the equation x² + y² = 1 corresponds one to one to a line through the point (-1, 0) with rational slope that. The solution is easily visualized if one uses geometry and views the equation as defining a unit circle.
Finding relationships between important invariants by capturing the essence of the problem
The polylogarithm, on which Dr. Bannai focuses, is a kind of which we call a “geometric object.” To better explain its concept, we interpret a “geometric object” as some sort of “figure.” If one has a figure, it is possible to derive various invariants, such as the “area” and “the number of vertex.” Therefore, suppose there are several invariants which you wish to compare. If one could find a figure that intrinsically contains these invariants, then this figure would be the starting point for finding some relationship between the various invariants. In a sense, the polylogarithm is a figure that intrinsically contains important invariants in number theory. “Suppose you can represent an invariant ‘A’ as a simple figure by abstracting its properties. Using the same technique, one next studies another invariant ‘B’ which looks completely different from ‘A.’ If one can express the invariant ‘B’ using the same figure as that of ‘A,’ then we can hope to find a formula or rule that governs both A and B.” Alexander Grothendieck(*2), who contributed greatly to algebraic geometry, referred to such geometric objects obtained through abstraction as “motives.” The polylogarithm is an important example of a “motive,” which plays a vital role in arithmetic geometry (Fig. 2). Dr. Bannai adds, “The term ‘motive’ used by Grothendieck comes from a commentary of the work of Paul Cézanne(*3). The post-impressionist painter Cézanne distanced himself from impressionists who depicted objects using the ever changing quality of light and shadow. Cézanne instead establish his own style emphasizing the “vital intensity that the motif possessed in its actual existence.” The ‘motive’ in arithmetic geometry also sees through the surface and captures the true essence.”
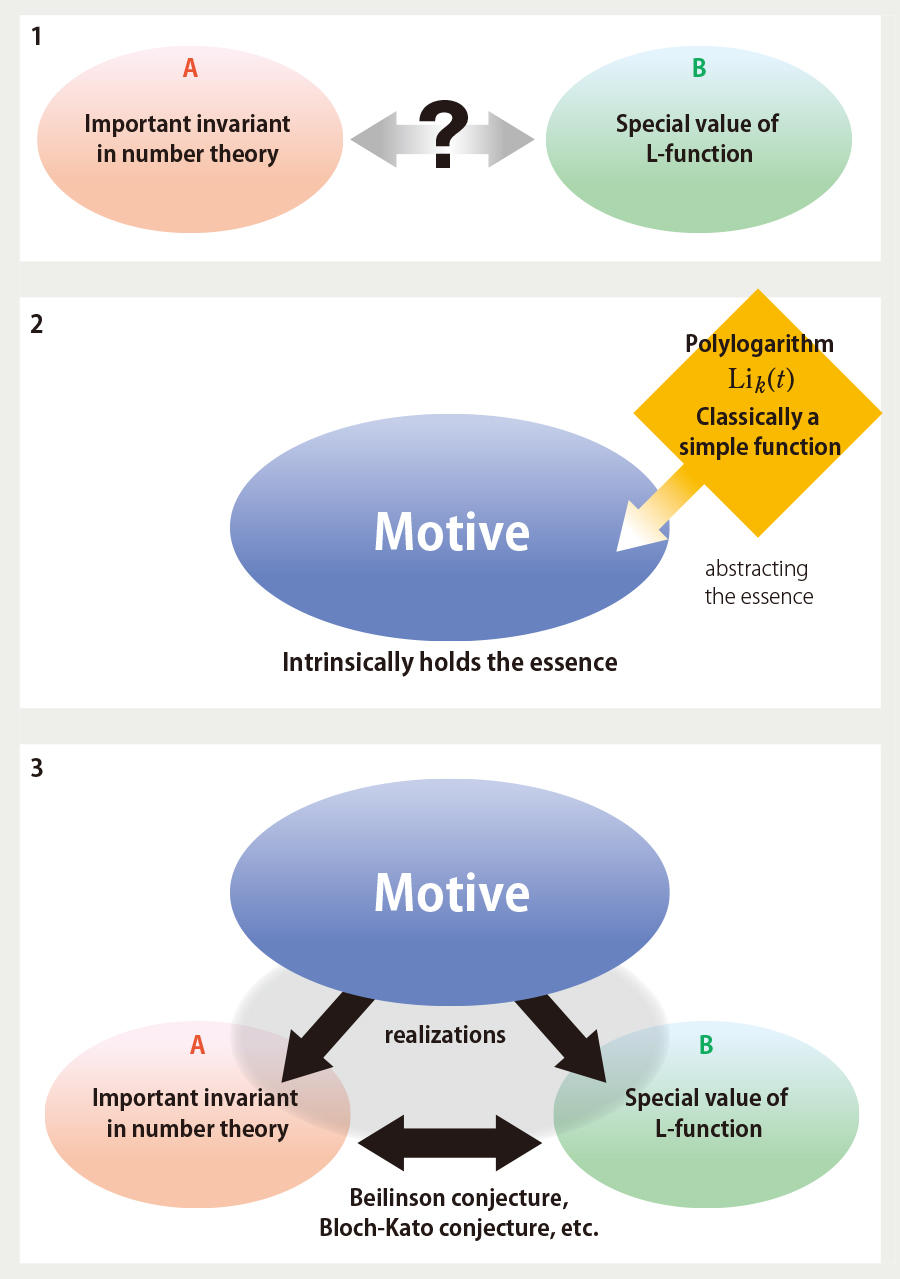
Fig. 2 Polylogarithm at work
(1) We consider “An important invariant in number theory” and “The special value of an L-function” – two invariants which appears unrelated to each other. (2)By starting from and abstracting the polylogarithm function, we construct a “motive” which gives a higher conceptual interpretation of the two invariants. (3) By going through the “motive,” we are able to find the relationship between two invariants which at first seemed unrelated. Such relationships may derive solutions to problems, such as the Beilinson conjecture and the Bloch-Kato conjecture.
Solving mathematical problems through cooperation
In stark contrast to the depth of his research, the reason Dr. Bannai chose the polylogarithm as his research topic seems very simple.
“I chose this theme because I was attracted by its simplicity,” says Dr. Bannai smilingly. One may imagine mathematicians as working alone when doing research. In reality, this is not the case.
“Remembering struggling through mathematics in high school, one may have the impression that mathematical research is a solitary endeavor. However, in reality, mathematical research typically advances through discussions among mathematicians around the world. Mathematics is a highly internationalized field of study. For example, my recent series of work is a joint project with Prof. G. Kings of Regensburg University in Germany. The situation is the same in my lab. While everyone has their own theme, members advance their studies through active discussions. They are taking advantage of being in a group and are enjoying its benefits.”
Dr. Bannai believes that polylogarithm will play a key role in understanding important problems in number theory. Above all, he is fascinated by the idea of finding unified rules through abstraction of various properties and quantities. He dreams that such methods would give clues to solving important conjectures.
Interview
Associate Professor Kenichi Bannai
“Nausicaä of the Valley of the Wind.” motivated me to return to Japan
You spent your childhood in the United States. Since when?
Since when I was 2-years old. Both of my parents are mathematicians, and our family moved to the States in the mid 70’s when my father was offered a position at the Ohio State University. Except for two years of kindergarten, I lived in the States until I returned permanently to Japan near the end of high school.
Growing up in the States, did you consider going to an American university?

At the time when my family was thinking about returning to Japan, I had graduated early from high school and received offers from several American universities to attend. It was in the late 80’s, when the world was feeling threatened by the rapid rise of the Japanese economy. Japan was portrayed as a country whose people were forced to work like machines all year around. Viewing repeated TV footage showing Japanese employees exercising in unison, I received the depressing impression that Japan was a country without freedom or individuality. Then one day, I encountered Hayao Miyazaki’s film “Nausicaä of the Valley of the Wind.” It was a fantastic visual depiction of an ecosystem totally different from our world, and I was totally overwhelmed by the force of imagination that could create such a world. This experience deepened my interest in Japan, and influenced my decision to return to Japan with my family.
Viewing Mathematics as an important tool in understanding the world
Why did you become interested in mathematics?
I started seriously thinking about mathematics in high school. At the time, I was interested in a wide variety of things. After hearing about Eisenstein’s theory of relativity, I wished I could study Physics; after learning about mathematical models of the ecosystem, I wished I could apply this to make mathematical models of human society; I wished I could create a good Artificial Intelligence program and become friends; I thought about creating a language more accurate and descriptive than any natural language; I wished I could propose a perfect social system to achieve world peace; I wanted to write scripts for movies and novels – I really wanted to do everything. I felt that I did not want to restrict my options, and was looking for some feasible solution. Then, something happened which made me think that mathematics may be good.
It happened during a class in chemistry; I came across a differential equation describing the change in concentration of a substance during a chemical reaction. It was an equation I had just learned during a class in mathematics, but at first, I did not think much of it. Then immediately after, during a university biology class that I attended, when calculating the growth of a population of an animal in a certain ecosystem, I again encountered the exact same differential equation. “Wow!” I thought. Furthermore, I saw the same equation being used in an economics class. In other words, I found the exact same abstract mathematical equation used with a specific meaning in a wide range of fields. I was convinced that mathematics would be useful in doing anything.
This conviction was further enhanced by Hermann Hesse’s novel “The Glass Bead Game”(※). This novel is a story about the future and is written as a biography of a master of the “Glass Bead Game” – an intellectual artistic “game” created by integrating mathematics, laws of physics and chemistry, music, poetry and other forms of art. I felt that through mathematics, I would be able to understand not only phenomenon in chemistry, biology and economics, but also music, literature and other forms of art!
You said you noticed that mathematics was being used in many fields. What do you think now that you are an active mathematician?
Mathematics has the capacity to abstract and draw out the important essence of things and events. I believe that in this increasingly complex modern society, mathematics can play a major role by using its power of abstraction. For example, there are situations where people have so many different opinions that it may seem impossible to come to an agreement. However, if we think deeply about what each person wants to achieve, we may realize that in fact, the goals are actually very similar. Even in cases where specific methods or situations are so different that negotiation seems impossible, if we capture the problem in a sufficiently abstract way, we could achieve a common ground and begin to discuss how to solve the problem in a calm and rational manner.
Although mathematics itself mainly deals with such objects as equations and geometric figures, I am beginning to realize that the mathematical approach to problem solving, including the method of abstraction, is potentially a powerful instrument in solving real world problems.

To realize the full potential of mathematical thinking, I want to introduce to society many more people who have acquired through mathematics various methods of problem solving. Through this effort, I am hoping for example that an organization incapacitated by becoming too large and fractured may find a leader capable of abstracting the needs of the various branches of the organization and finding a unified goal to propel itself forward.
Therefore I would like for my students to learn not only techniques for solving specific problems at hand, but to properly learn very abstract mathematics. A specific solution to a concrete problem in many cases is harder to apply to other situations, and often the problem itself is difficult to solve because there may be many factors hiding the true problem. Abstract mathematics may at first appear difficult to understand, but its clarity and its applicability is spectacular!
(※) “The Glass Bead Game” is a novel by Hermann Hesse, a German writer.
Dealing with family and students with the same affection as I do with mathematics
What do you do when you are not doing research?

I’ve always enjoyed spending time with my wife. After the birth of my daughter two years ago, my family life is even more fulfilling. However, I don’t feel that time with my family is separate from the time I spend doing mathematics. I feel I’m thinking in the same way – when engaging in research, dealing with my students, or enjoying playing with my daughter. Dealing equally with mathematics and my dearest daughter may sound as though I am a bit too cold as a father, but I feel that I have the same great affection for mathematics as I do for my daughter. Thinking about the essentials of how to associate with or how to establish proper relationships with people has become so much fun that having such an abstract perspective or a mindset based on mathematical speculation is now almost a hobby for me. On the other hand, we have to remain cautious about careless generalizations disregarding reality and actual phenomena. For example, one could cause a disaster by dogmatically applying a general educational principal in a certain teaching situation without fully understanding the principals involved or the subtlety of the situation. The reason I believe many people are weary of arguments coming from abstract theory is the prevalence of such careless generalizations. When we use an abstract theory in mathematics, we check very strictly that the specific situation satisfies the conditions making the abstract theory applicable. I think it is very important to form the habit of checking rigorously in each specific situation to see if abstract argument is indeed applicable.
What do you think are good points of Keio University?
First of all, the students are very highly motivated. While I was staying in France in 2007, I had the opportunity to participate in a number theory workshop known as the UK-Japan Winter School jointly sponsored by Cambridge and Keio universities. I was very impressed with the enthusiasm of Keio students.
At many Japanese universities, the department of mathematics belongs to the faculty of science. Furthermore, at the University of Tokyo where I studied and Nagoya University where I previously worked, Mathematics belonged to an independent graduate school, which made me feel somewhat isolated from other departments. At Keio University, the Department of Mathematics belongs to the Faculty of Science and Technology, allowing us to be in close contact with the technological departments. I have many opportunities to discuss with faculty from other departments – an advantage creating a health synergy between science and technology. Such a campus environment is probably one reason we have many creative and lively students.
Student A : Prof. Bannai is free of the stereotypical image of a mathematician. He is always willing to advise us even on simple questions and is open-minded enough to take interest in what we say or ask. This broad-mindedness makes his character very attractive. During lectures, he is very enthusiastic and inspires us to study mathematics. When we become stuck with a problem, he kindly gives us hints, often in a subtle manner, to help us along.
Student B : Prof. Bannai is fond of new things and is active enough to get out of campus to check it out himself. Recently he told us about visiting a manufacturer’s showroom in trying an electronic whiteboard; after returning to the lab he enthusiastically explained his impression of the whiteboard. He talks about his interest openly, and laughs when he finds something truly interesting. He is very friendly and reliable mentor.
(Reporter & and text writer: Kaoru Watanabe)


