- Home
- New Kyurizukai
- Pure Mathematics
from Keio's Faculty of Science and Technology
Pure Mathematics
from Keio's Faculty of Science and Technology
In quest of truth that mathematical objects have
Taking up the pure mathematics career led by friends I met during the Math Olympiad, and by my respected teachers
Dr. Katsura says he was first induced into mathematics by friends whom he met during the Japan Mathematics Olympiad and studied together with them before choosing the career of a mathematician. Later, he met co-researchers from other disciplines and teachers under whom he would study. In addition to these assets, also supporting Dr. Katsura, now as a researcher, are various valuable experiences he gained in Japan and overseas as well as his family.
Takeshi Katsura
Born in Kyoto, Dr. Takeshi Katsura specializes in the C*-algebras, a field of the operator algebra theory. In particular, he focuses on C*-algebras related to dynamical systems and the set theory. In 2003, he completed the doctoral course at the Graduate School of Mathematical Sciences, the University of Tokyo. Doctor of Mathematical Sciences. After serving as a postdoctoral fellow at the Hokkaido University, University of Tokyo and University of Toronto, Dr. Katsura assumed a spost as an assistant professor of Keio University Faculty of Science and Technology in April 2008, then assumed the current post as an associate professor in April 2012.
The Research
Associate Professor Takeshi Katsura is Featured in this issue, whose field of research focuses on the theory of C*-algebras, a field of pure mathematics.
The fundamental motivation for mathematics lies in “Beauty”
What is the attraction of the pursuit of pure mathematics?
Of the many academic disciplines, mathematics is one of the most indispensable as the foundation of our civilized society but is perhaps the least understood by people due to its breadth and depth. Particularly, the field known as pure mathematics – which is in the opposite end of practical sciences – is a world extremely hard to see and a world that only a handful of specialists can deal with. For this issue, we asked Dr. Takeshi Katsura about the attractiveness of and his approach to pure mathematics, and some of the theory of C*-algebras which is his specialty.
Solving problems is not all about pure mathematics
We sometimes hear of news bandy around like this, “A mathematical problem, which has been unsolved for centuries, has been solved at last!” But it is often the case that understanding how such a difficult problem was solved is extremely difficult even for specialists and can take years to examine whether the proof is correct. Such is a hardto-understand aspect of the world of pure mathematics. Then, how are mathematicians solving problems?
“Of course I admit that solving problems is the mainstream of endeavors for studying pure mathematics. On the other hand, in pursuing studies we mathematicians rarely experience solving a problem truly worth solving. This is because many of the problems that remain unsolved by humans are either totally worthless or ones too difficult to solve. It is also true that too difficult a problem to solve is not always well worth solving. Many scientists then scrutinize the value of a solved problem and its results over a period of many years. It can also happen that results of abstract pure mathematics studies are unexpectedly applied to practical uses after a century or two. That’s why I think we, researchers of pure mathematics, must establish and maintain values and an aesthetic sense of our own that are not affected by others and yet sympathized by them,” emphasizes Dr. Katsura.
If solving problems is very difficult as he says, then what are mathematicians advancing their own research for, and how?
“In the study of pure mathematics, I think much of our efforts are directed toward finding curious phenomena and understanding them, rather than simply solving problems and finding answers. To do so, we must thoroughly investigate the object, build a hypothesis and verify it through experiments. This approach seems similar to approaches taken in the engineering field. What characterizes pure mathematics is that our targets are abstract mathematical objects. Another characteristic is that we basically take an approach that we term ‘thought experiments’ although experiments often depend on computers.”
He continues, “No matter how acceptable an answer appears, it cannot be considered to be the ‘result’ unless it is proven properly. This is still another characteristic of mathematics. Suppose you have found a phenomenon to be proven but are unable to prove it. In that case you may publish it in the form of a conjecture, but even so it is regarded as an important research achievement in mathematics. Some day in the future, I’d like to publish a conjecture that would lead mathematical studies of the world. Of course, it would be best if I could prove it.”
Noticing structures of sets and examining their relationships
How is it possible to investigate into mathematical objects that are both invisible and intangible? The keywords are sets and structures, according to Dr. Katsura.
“When asked about the most familiar mathematical objects, everyone will answer they are numbers such as natural numbers, integers and real numbers. In investigating into numbers, there is an approach: to collect and examine a set of all numbers that satisfy certain properties, instead of dealing with each individual number. In mathematics, we call a collection of such mathematical objects a ‘set.’ For example, a set of all natural numbers is represented by N, which is an infinite set. On the other hand, a set of all real numbers, R, is often expressed as a number line.”
“These sets of numbers naturally have their own ‘structures.’ For example, a number line as an expression of a set of all real numbers, R, is considered to express structures such as a ‘relation’ for two real numbers – which is large and which is small – and a ‘metric’ between the two numbers. Besides these structures, sets of numbers have a structure known as ‘operations’ that involves addition, multiplication and so on,” Dr. Katsura mentions.
He says it is possible to shed light on the very structures by describing these various types of structures in set-theory languages like mapping (*1).
“E ach time we notice a certain structure, the set having that particular structure becomes a research object in mathematics. For example, the structure ‘metric’ leads us to concepts such as metric spaces and topological spaces (*2), which are the objects of geometry. Likewise, the structure ‘operations’ involving addition and multiplication leads us to concepts such as “groups,” “rings” and “fields” (*3), which are the objects of algebra. In today’s pure mathematics study, it is common to look for instances of such mathematical objects and investigate into relationships between properties shared by such objects and those between different objects,” Dr. Katsura continues.
In particular, Dr. Katsura shows a special interest in and focuses on relationships between objects of different structures (ring, metric space, etc.) and objects having multiple structures (group, topological space, etc.) at the same time.
“Up to now I have focused on the object called ‘C*-algebras’ (*4). In addition to structures such as metric spaces and rings mentioned earlier, C*-algebras also have structures called linear spaces and ‘*’ (star) and satisfy various conditions (*5) among these structures. While intriguingly interrelating with other objects such as dynamical systems (*6), topological spaces and fields, C*-algebras are being studied even today. I personally regard C*-algebras as very charming, but I cannot explain it in compact, easyto-understand expressions. Because easy explanations often come with incorrectness and falsehoods, you know,” says Dr. Katsura smilingly.
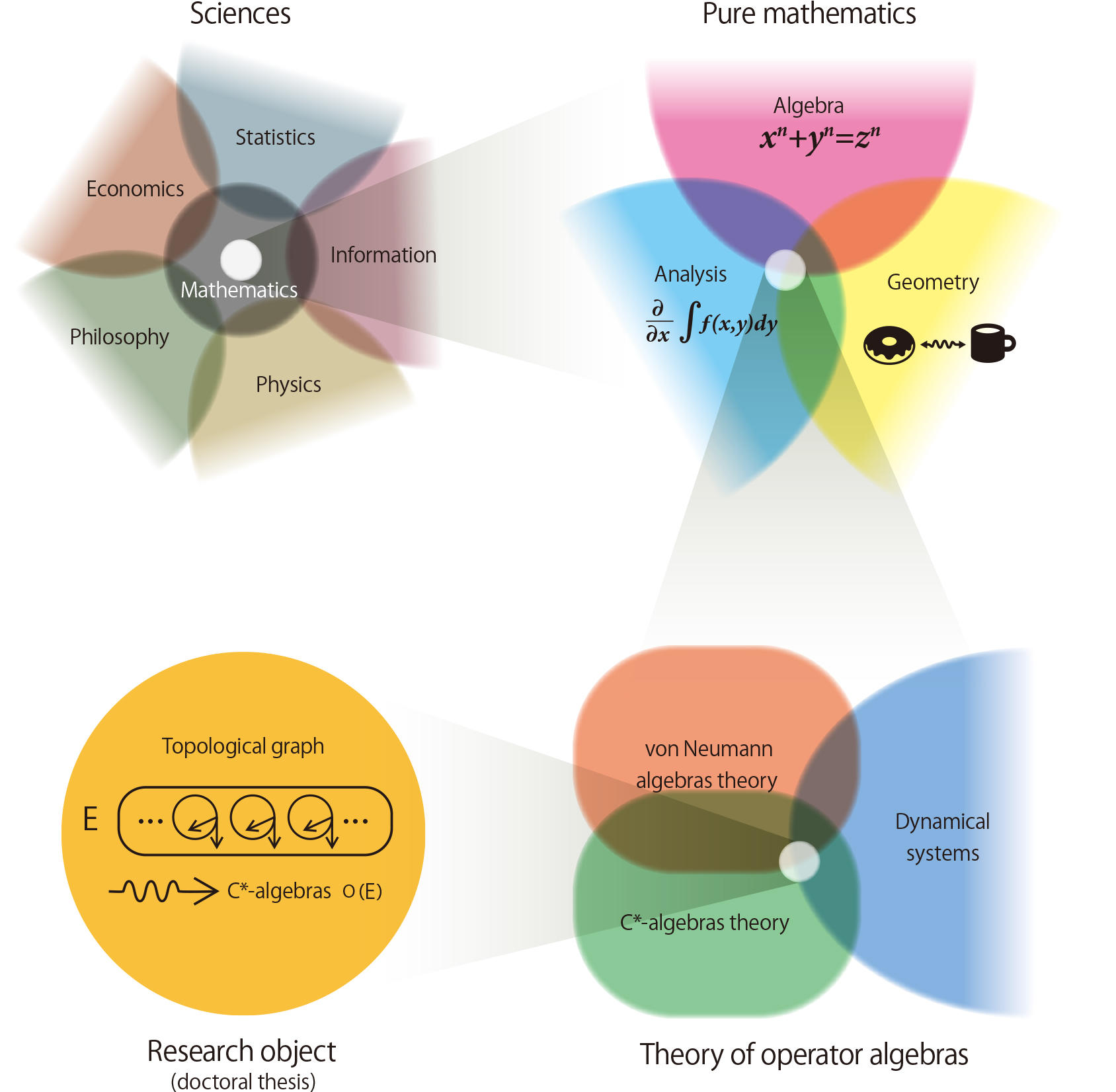
Fig. The positioning of Dr. Katsura’s doctoral thesis and related fields
Generally speaking, mathematics is related to diverse fields, but Dr. Katsura’s specialty is “pure mathematics” seemingly having little to do with the other fields. Yet, he maintains an interest in aspects of pure mathematics that are concerned with other fields. In his doctoral thesis, he introduced a new perspective into an area where “C*-algebras” in the theory of operator algebras meet dynamical systems related to physics. He is now becoming more interested in set-theory-oriented mathematics, a field said to be close to philosophy.
I’d like to open up a new horizon of mathematics by challenging boundary areas
What meaning does Dr. Katsura find in studying the highly abstract world of mathematics? “For me, the foremost motivation is that I feel ‘beauty’ in there. In fact, while I’m wrestling with a question, there happens to be a moment when I find a truth that I feel truly exquisite. In the 19th century, mathematicians discovered an extremely beautiful area of mathematics called complex analysis (*7). In the 20th century, this complex analysis played vital roles in mathematical description of quantum mechanics by von Neumann and others, the results of which have supported our modern society through semiconductors. In this manner, it is often the case that truly beautiful mathematics can find unexpected applications after many years. I’d like to leave such a significant achievement to posterity myself,” talks Dr. Katsura eagerly. He also expressed prospects that he would like to pioneer yet unexplored fields of mathematics by expanding his research objects beyond C*-algebras to cover boundary areas of dynamical systems, number theory and set theory studies.
Interview
Associate Professor Takeshi Katsura
I was rather good at arithmetic but not at calculation
What was your childhood like?
I was born and raised in Muko City, a so-called “bedroom” suburb community in Kyoto Prefecture. My father was so fond of board games and puzzles that all sorts of playthings, such as Othello and backgammon (board games) and Rubik’s Cube, were everywhere in my home, with which I used to play almost everyday in my childhood. It was customary that I enjoyed board games together with my family members.
That said, I also liked playing outdoors as an elementary schoolboy. In my junior and senior high school days, I belonged to the Soccer Club. As for other types of pastime, I liked playing mahjong (Laughter).
We guess you were good at arithmetic since childhood, is that right?
I was good at arithmetic but not at calculation at all. Even today, calculation is my weak point. What I liked were puzzle-like problems and diagram-based problems like those often set in IQ tests.
I experienced a regretful setback when I was taking a test for admission to a junior high school. Despite months of hard work preparing for admission to Rakusei Junior/Senior High School, I struggled with one arithmetic question I simply couldn’t solve. So attached to that question, I had little time to review the other questions, which resulted in many calculation mistakes. Prior to that entrance exam, I had already passed the entrance exam for Todaiji Gakuen School, in which I was the only successful one among my friends who took the exam. This may have made me somewhat off guard. After all, my friends were admitted to Rakusei and I was the only one going to Todaiji Gakuen. Due to its unrestricted school culture, the Todaiji Gakuen School allowed me to study freely, which proved good for me as a result. Since that time, I’ve made it a rule to take other approaches and check my answers to math problems three to four times. The bitter experience in the junior high school entrance exam was a good lesson for me after all (Laughter).
About when did you make up your mind to focus on mathematics?
Toward the end of my high school second year, I was chosen as one of the twenty Japanese candidates for the International Mathematical Olympiad (IMO). This event turned out to be an opportunity for me to find fun in pure mathematics for the first time in my life. Joining the screening camp, I was surprised to find a number of extremely bright fellows who were as well versed in mathematics as being able to see through to the point of the problem. Until then, I had never met students of my age who were better at mathematics than myself, which was a tremendous stimulus.
At that time, I was left out of the final selection of six representatives to my regret. However, in the summer of my third year of high school, I had an opportunity to participate in a camp mostly for IMO representative candidates. It turned out that some of the fellow students I met there would change the course of my life. They invited me to go to the University of Tokyo to study mathematics together, so I decided to go to the university instead of the nearby Kyoto University. Then I was admitted to the university’s Natural Sciences I, left for Tokyo and began living there alone.

After entering the university, I seldom attended classes. Rather I made it a rule to attend a weekly reading circle with those friends after deciding which textbooks to read. In those days, I was desperately voracious for mathematical knowledge, spending quite some time to study. Later, most of my friends in the reading circle chose careers as mathematics researchers. On the other hand, the six representatives, who actually took part in the Mathematical Olympiad, did not become mathematicians (Laughter).
Skipping a grade from junior to master's course
Then do you mean you devoted yourself to mathematics during your undergraduate years?

Not at all times. Besides studying mathematics, at the invitation by one of the reading circle friends, I took up a part time job as a math lecturer at a cram school, teaching university-class mathematics to junior and senior high school students. I was actively involved in the cram school, drawing up original curricula and creating textbooks of our own, for example. The experiences I gained at the time seem to have paved the way for what I’m doing now – teaching students.
I was also a member of an inter-college mountaineering circle, mingling with students from other universities. In a typical itinerary of three nights and four days, we climbed 3000-meter-class mountains such as those in the Southern Japan Alps, carrying a tent of our own. Some of the circle members were from Keio University. I made a friend of Mr. Kenichi Tanaka from Keio (now Associate Professor, Keio University Department of Administration Engineering) in the circle activity. Just as with the case of Dr. Tanaka, I met my future wife through this circle.
You skipped a grade when you were an undergraduate, didn’t you?
Yes. Again at the invitation of those friends, I challenged the grade-skipping exam, an opportunity allowed only for juniors. All of us passed the exam, so we quit the undergraduate course halfway in the third year and advanced to the master’s course. While two of my friends chose the number theory, I joined the lab of Professor Yasuyuki Kawahigashi who specialize in the operator algebras theory.
At the Kawahigashi lab, we were required to speak without looking at notebooks. At my own lab, we are following suit with this style of learning. It was a tough practice in the beginning, but I soon found that it is a superb method to accurately understand the problem and nurture the ability to restructure the problem – far from compelling us to memorize things. Not limited to mathematics, training yourself in this way will be surely useful even after you go out into the world.
In the second year of my master’s course, I studied abroad at the Mathematical Sciences Research Institute (MSRI) near the University of California, Berkeley for a little less than a year.
Returning to Japan, I completed two years of doctoral course before getting married. Then I continued research activity at the Graduate School of Mathematical Sciences, the University of Tokyo in the capacity of a postdoctoral fellow (PD) of the Japan Society for the Promotion of Science (JSPS). During this period, I also experienced an extended stay in Oregon, U.S.A. Then, I had an opportunity to spend three enjoyable years of research at the Hokkaido University Graduate School of Science (Faculty of Science) as Superlative Postdoctoral Fellow (SPD) of JSPS. Those three years were fruitful as I could fly around the world and cultivate valuable human relationships, which became the foundation supporting my current research activities.
There is one more thing I gained during the years at the Hokkaido University. Inspired by the manga “Hikaru-no-Go,” I was awakened to the fun game of “Go”. Currently, I’m a third grade rank holder of Go.
Passing through a narrow gate to become an assistant professor of Keio University Faculty of Science and Technology
While mathematicians today are in great demand by businesses, it is said finding employment is difficult for mathematics researchers
Because securing a post as a mathematics researcher is highly competitive, one needs good timing and luck in addition to ability. When I completed the doctoral course, an increasing number of young people wanted to become researchers but the number of posts available was on the decrease. Naturally, they were faced with keen competition. In my case, following the service with the Hokkaido University, I had to serve as a PD at the University of Tokyo for half a year then at the University of Toronto. Since I got a preliminary offer for a post from Keio just before leaving for Toronto, I put an end to my six months of stay in Toronto much earlier than the initial plan. In April 2008, I reported to Keio University Department of Mathematics, Faculty of Science and Technology as an assistant professor. Because I was able to find employment with such a highly reputable university as Keio, I feel the five years of my PD period were not useless after all. After assuming a post with Keio, I also had a chance to study at the University of Denmark.
A good thing about Keio University Faculty of Science and Technology lies in that the relation between teachers and students is close, reflecting the Keio policy of “Half Learning, Half Teaching.” When it comes to study we have hot discussions, but enjoy sake together at other times in an at-home atmosphere, which I like very much. Unlike mathematics departments of other universities (Japanese or overseas) I know, Keio’s Department of Mathematics not only pursues pure theories of mathematics but also emphasizes application aspects of this study. Of our students, only a few become mathematics researchers after graduation. Their future courses are diverse, some becoming school teachers and others finding employment with businesses and so on. At Keio, interactions among teachers from various departments, such as labs specializing in statistics and computer sciences, are also active. Speaking of myself, I feel my field of vision has expanded considerably thanks to such an open culture.
Do you sometimes engage in joint researches yourself?
Yes. I studied alone in the beginning. But while I was in Toronto, a set theory specialist, who had read my paper, visited my office and offered a joint research on a certain problem. It was a difficult problem left unsolved for 30 to 40 years. By joining forces, however, we could solve that problem. Since that time, I’m willing to call out to other researchers when I feel joint research approach would be better.
On what occasions do you usually get inspiration?

When trying to solve problems, the first thing I do is find out things in common in several instances and phenomena and then arrange them in writing. Thinking it over for some time, there may come a moment of inspiration while I’m relaxing. Or it may come while I’m taking a shower, or walking. Such moments vary according to the situation. One day I suddenly got an inspiration. So excited with joy, I phoned up my co-researcher in spite of myself.
This is why the existence of my family, with whom I can relax in comfort, is so important. I have a family of four: my wife who is my good supporter, the first son who is an elementary school third grader, and the second son who is a preschool senior class student. The first son is already a third grade rank holder in the game of Go, the same level as me. He defeats me at times (Laughter). He was even chosen as a Go representative for Kanagawa Prefecture. The second son loves playing board games just like myself and is getting stronger and stronger. I’m proud of him and looking forward to his future.
Some words from students
Student : I joined the Katsura lab simply because Dr. Katsura’s class lectures were overwhelmingly interesting, where I could image even difficult problems in an understandable way. It’s a tough requirement that we shouldn’t look at notebooks when speaking in seminars. But this rule helps me a lot in understanding things accurately and speaking logically in public.
(Reporter & text writer: Madoka Tainaka)


