- Home
- New Kyurizukai
- Operations Research
from Keio's Faculty of Science and Technology
Operations Research
from Keio's Faculty of Science and Technology
Modeling and optimization of social systems
Encounter with administration engineering led me to follow a researcher’s career.
Dr. Tanaka says as a child he liked playing amid nature and was extremely inquisitive. However, a dream of becoming a researcher never occurred to the boy. What drastically changed the course of his life was an encounter with administration engineering as a field of research. Approaching highly complex social phenomena, administration engineering aims to solve problems by developing mathematical models and offering concrete solutions to practical problems. Dr. Tanaka explains that this discipline is appealing partly because it has the powerfulness of making specific solutions to real-world problems, something which is common to engineering, and partly because it offers scientific excitement common to physics which describes natural phenomena by simple laws.
Ken-ichi Tanaka
Dr. Ken-ichi Tanaka was born in Tokyo, Japan. His specialties are operations research and social systems engineering. After graduating from Keio University Department of Administration Engineering, Faculty of Science and Technology in 2000, he completed the master’s course at Keio University Graduate School of Science and Technology in 2002, then completed the doctoral course at the same graduate school in 2005 (Dr. Eng.). He became a research associate at Tokyo University of Science Department of Management Science, the Faculty of Engineering. Then he served as an assistant professor for the Department of Systems Engineering and then for the Department of Informatics at The University of Electro-Communications. In April 2014, he became an assistant professor at Keio University Department of Administration Engineering, Faculty of Science and Technology. In April 2016, he was promoted to the current position as an associate professor of the same department.
The Research
Associate Professor Ken-ichi Tanaka is featured in this issue, whose field of research focuses on solving urban and regional problems via mathematical approaches.
Using mathematical models to derive optimal location of facilities and their operating hours
Modeling and optimizing social systems
Operations research (OR) is a discipline that uses mathematical methods to work out rational plans for or present optimal solutions for diverse social problems. Dr. Ken-ichi Tanaka is devoted to research that helps determine, via mathematical approaches peculiar to OR, optimal locations of public and commercial facilities and their optimal operating hours. By showing that convenience and profitability of facilities are largely affected by their locations and operating hours, OR allows facility administrators to make rational decisions. In this sense, OR is a highly practical discipline and is often referred to as a science for decision-making or a discipline for problem solving.
Introducing the time axis in facility location problems
The Department of Administration Engineering, to which Dr. Tanaka belongs, focuses on problems arising in such divers e are as as f inance, information, and infrastructure, and seeks to provide solutions to the problems using mathematical approaches. Given the target research theme – the whole social system – being comprehensive in scope, it naturally concerns diverse fields and involves hard-to-handle aspects. OR is a highly practical discipline capable of presenting concrete solutions to problems related to society.
Of the diverse fields of OR, Dr. Tanaka specializes in “facility location problems” in the field of urban engineering. Dr. Tanaka explains the characteristics of his study as follows:
“More than a century has passed since the first facility location problem was proposed, which is now known as the Weber problem that seeks an optimal location of a facility such as a factory. Facility location problems have been extended in a variety of directions to deal with more realistic situations. Basically, however, most facility location problems have ignored the temporal dimension and have focused on static and deterministic problem formulations. What makes my research approach unique is incorporating the behavior of people into the model who wish to consume services at the facility within a limited period of time by considering the temporal dimension.”
Dr. Tanaka proposed dynamic location problems that seeks to determine the optimal start time of services at facilities as well as their locations. As an example, the problem can be applied to determining how to provide afterwork lectures to commuters who wish to study at graduate school. In addressing this problem, he assumed a case where employees of companies in the Tokyo metropolitan area drop in at the graduate school on their way home from their workplaces. Then he derived an optimal facility location and a desirable classstarting time that maximizes the number of users – an attempt to facilitate the decision-making process on the part of the service provider.
“Too early a starting time would result in less students who could attend classes in time after leaving their workplaces. But too late a starting time would make it difficult for them to return home by a desired time. By focusing on such tradeoff on the time axis, the key point is to determine optimal service start times for facilities as well as locations,” Dr. Tanaka mentions.
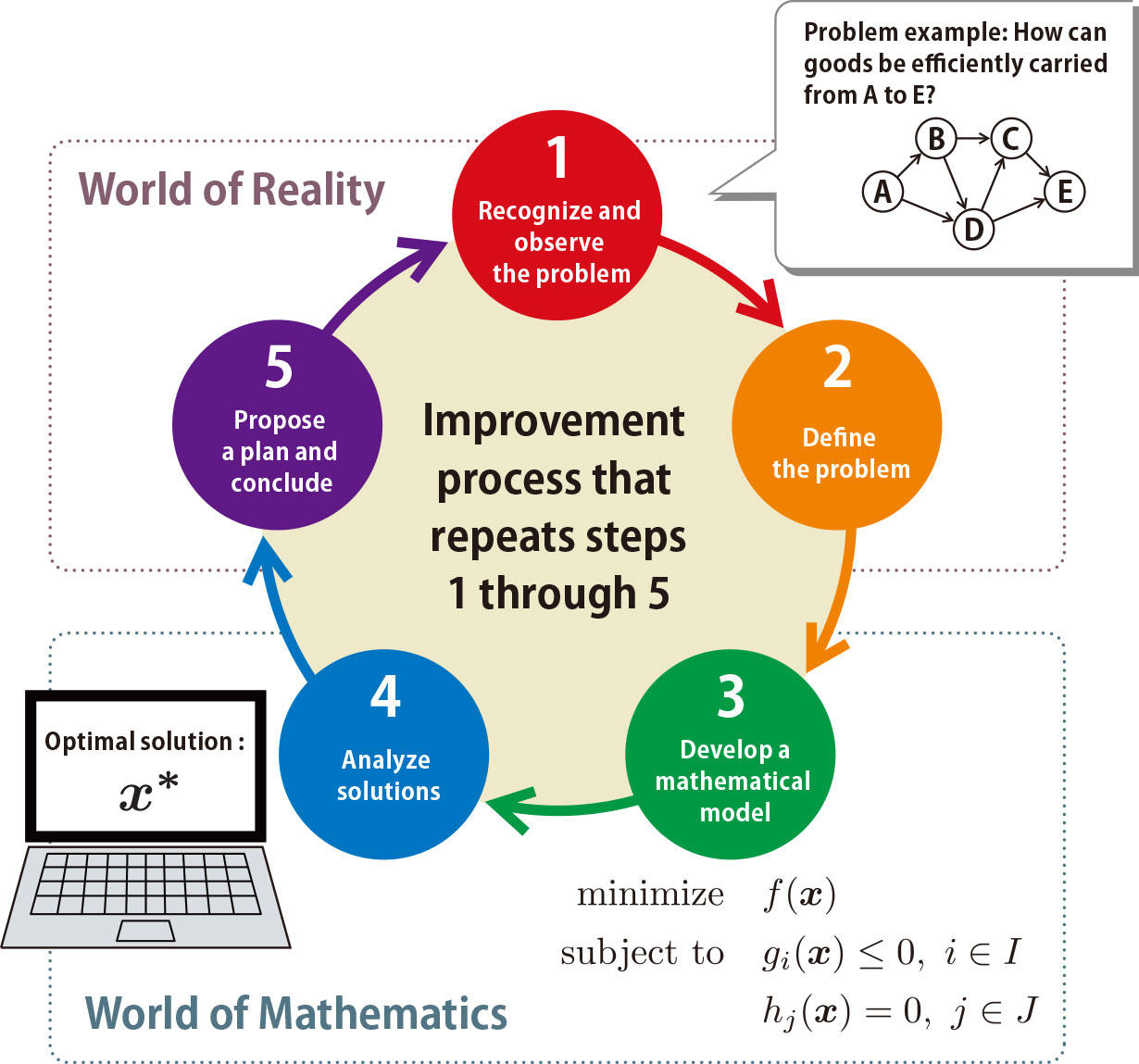
Fig. 1 Process of problem solving using mathematical models
The key point in developing a mathematical model is to focus only on important factors of the target under study, and formulate the situation as a mathematically easy-to-handle problem. The aim of mathematical modeling is to provide useful knowledge for decision-makers. The flow of steps 1 through 5 is repeated as long as time and cost permit.
Mathematical methods often provide good solutions, which could not be easily found by intuition and experience
To proceed with the challenge, Dr. Tanaka decided to use the “Census data for commuter traffic in Tokyo metropolitan area” – large-scale data based on a questionnaire survey of trains and buses used for commuting in the Tokyo metropolitan area. Based on the data, Dr. Tanaka developed mathematical models to determine: where in the metropolitan area should the graduate school for after-work commuters be located and at what time should the classes be started. The aim is to maximize the number of commuters who can attend classes for three hours after leaving their workplaces and return home by 23:00
“But this attempt was not without a problem. Compared with merely locating the facility, inclusion of the time axis involves an incomparably larger amount of information to be handled. While a variety of solvers (software programs) are already available to solve mathematical optimization problems, even the latest solvers are unable to handle such large data volume due to inclusion of the time axis. To tackle this challenge, not only did I devise mathematically tractable models but also designed a special algorithm that exploits the structure of the proposed model,” Dr. Tanaka adds.
Assuming that class start times can be chosen from candidate set with every 10 min from 17:00 and 20:00 and only one location is selected in Tokyo metropolitan area, it was found optimal to locate the graduate school near Shinjuku station and start the classes at 7:10 p.m. The second and lower choices were Shibuya, Omotesando, Harajuku and Yoyogi in that order, which confirms our intuition. Interesting results were obtained when the number of facilities was increased to two or more. Let’s look at a case of two facilities. If the class starting time can be set independently for each facility, it was found optimal to locate schools in Shinjuku and Aoyama-itchome and start at 7:30 and 7:00 p.m., respectively. In the case of starting classes at the same time, the optimal result was to locate schools in Jimbocho and Kikuna (Yokohama) and start at 7:10.
He continues, “If it’s possible to set class starting times independently for each facility, it was found advantageous to locate several facilities simultaneously in Tokyo’s city center and stagger starting times. On the other hand, if classes need to be started at the same time for all facilities, it was found better to locate facilities not only in the Tokyo city center but also in residential areas not far from service beneficiaries’ homes. Optimal solutions thus vary widely according to the rules to operate facilities. As this example suggests, mathematical approaches can often provide rational, effective solutions, which cannot be easily found by intuition and experience. I think it’s the fascination and power of mathematical modeling.”
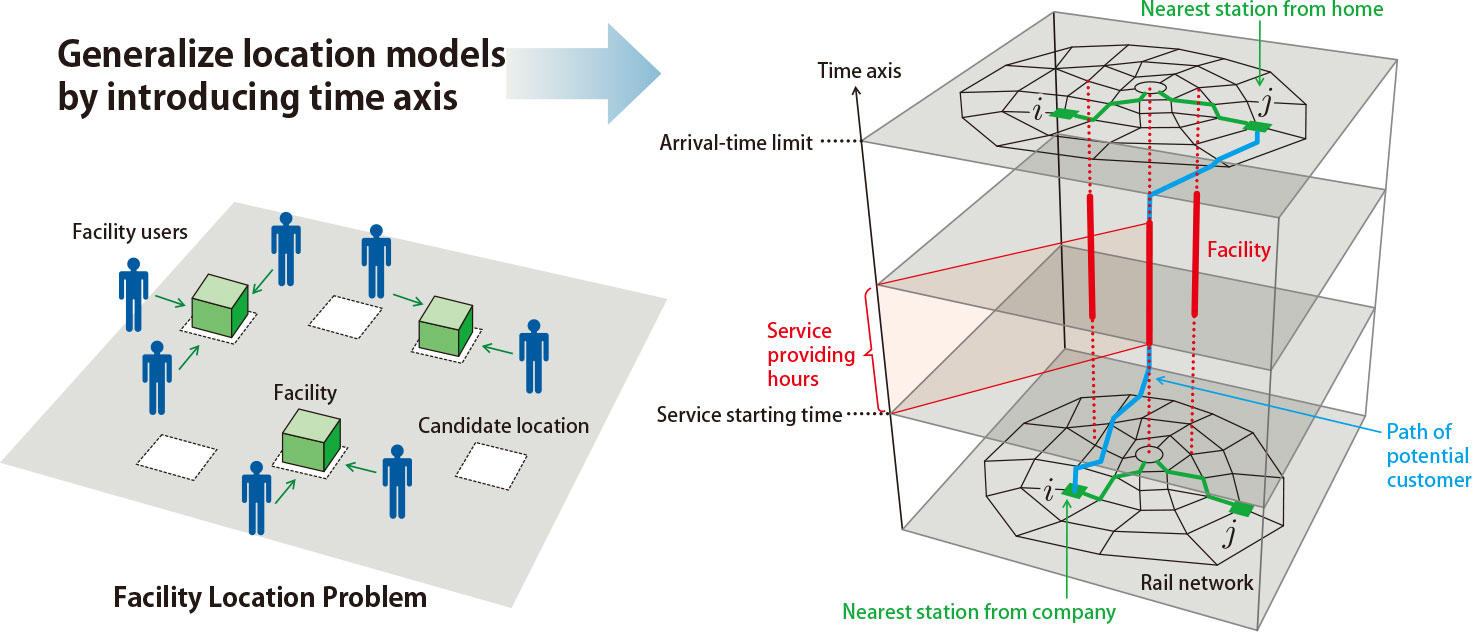
Fig. 2 Extending facility location problems by introducing time axis
Time axis is usually ignored when discussing facility location problems. However, temporal factors are important considerations when evaluating the accessibility of the facility. Fig. 2 generalizes the situation by introducing the temporal dimension into a physical network such as railway, road, and other networks. By describing the movement of people (commuters’ behavior to access facilities) and the provision of services at facilities in the spatial-temporal dimension, various types of important location problems can be considered. This approach is aimed at building a general framework that can be applied to a wide variety of situations.
Wishing to present generic models useful for various situations in our lives
Dr. Tanaka mentions “the location and scheduling problem of the graduate school for after-work commuters is just one of the many instances with which the proposed dynamic location problem can be dealt.” The true goal is to create generic models applicable to a variety of situations.
He continues “but this particular model alone can be applied to a wide range of subjects, such as sports clubs, movie theaters, concert and other event venues, by changing the way users drop in at facilities, the rules to operate facilities and other conditions. In addition, this model can also be used to wider situations where decision makers review and improve operating hours of services at existing facilities such as libraries and nursery schools. In short, my ultimate aim is to present frameworks for analysis by creating generic models,” Dr. Tanaka stresses. This is why his research themes range widely.
For instance, Dr. Tanaka is recently engaged in a joint research theme on designing safe walking routes from school to home for elementary school children by making them walk together as a group. This study aims to minimize the sum of the distance each child has to walk alone while also trying to shorten all students’ total distance of travels between school and home so that they are not involved in accidents or incidents on their way home. As a result, it became possible to reduce the sum of the distance that each student must walk alone to about 60% while keeping the total distance traveled by all the students to an increase of less than 1%. Recently, this research result was published online in an international journal of high reputation.
Some of Dr. Tanaka’s projects underway are: energy-saving urban planning by considering users’ transportation model choices; urban infrastructure maintenance and management models focused on aging facilities; and location problems for emergency evacuation facilities to prepare against volcanic eruptions. Inspired by needs from realworld situations such as mentioned above, he develops new mathematical models and attempt to present concrete solutions to each problem.
“The use of mathematical approaches can lead us to unexpected discoveries, which is useful for building a better society. I’m highly motivated to continue working hard so that I can develop and deliver impactful research results to society,” Dr. Tanaka thus concludes with bright eyes.
Interview
Associate Professor Ken-ichi Tanaka
Showing exceptional spirit of inquiry into nature and interest in natural science
What was your childhood like?
I was born in Musashino City of Tokyo, where Nogawa Park, Koganei Park and Inokashira Park were found within several kilometers from my home. On holidays and during summer vacations, my father often drove a car to take me to nature-rich destinations like Yamanashi and Nagano prefectures, which also helped make me an outdoors-oriented boy. Insect hunting was my favorite pursuit, which I used to enjoy with my friends. I was particularly fond of stag beetles. Going to the sea, it was often the case that I was absorbed in watching small fish and crabs in a tide pool rather than swimming. I was also interested in stars and constellations. As an elementary schoolboy, I referred to astronomical picture books to memorize names of constellations and nebulas. Books about supernova explosions and black holes were also full of surprise. I remember I was too excited to sleep at night when thinking about the end of the universe (Laughter). All in all, I was a natural science freak throughout the elementary and junior high school days.
In the meantime, I had learned to play the piano in my childhood, influenced by my father who was an acoustic engineer and my mother who was a classical music lover. During my junior high school days, I even learned under a music college teacher, wishing to advance to a music college. It may surprise you to know that in those days I played piano for six hours or so every day. However, I quit piano lessons halfway after hesitating to decide which way to go. I’m now away from piano playing to my regret, but I’d like to take up playing piano as a hobby again some day.
Under such circumstances, I went to a local metropolitan high school. It was around that time that I was awakened to the fun and excitement of mathematics. It was really surprising for me to know that the area of a figure surrounded by a curve can be found by means of a manipulation called integration. Just at that moment, I found mathematics is a really fascinating subject – for the first time in my life. Looking back at myself, I seem to have had the inborn sensitivity to appreciate the fun of natural sciences and mathematics. But it doesn’t necessarily mean I got good grades in these subjects (Laughter).
That’s why you chose an engineering course rather than biology upon entering the university?

Well, the fact was I had no particular discipline in mind yet in those days. At Keio University, the Faculty of Science and Technology has the system in which sophomores choose a particular department to belong to. I chose the Department of Administration Engineering simply because it appeared somewhat interesting due to the diversity of areas it covers, such as humans, urban planning and social problems. After listening to some lectures, I found the approach used in administration engineering very interesting as it expresses social problems, human behaviors and other complex and “soft” targets mathematically and sheds light on their underlying structures. In those days, I was still interested in physics due to its ability to describe phenomena in the world in terms of simple laws. But after receiving lectures, I came to realize that administration engineering could also use the similar approach in dealing with real-world problems. I was lucky in that sense.
Awakened to fun of research as a senior after fully enjoying a campus life
Did you make up your mind to choose a researcher’s career when you joined the Department of Administration Engineering?

No, far from it. My future as a researcher never occurred to me in those days. What’s more, I was not so serious about learning until the end of the third year. In fact, I was enjoying a student life, doing a side job as a lecturer for a cram school, engaging in basketball, badminton and outdoor circle activities. Incidentally, my wife and I met at the outdoor circle.
I was awakened to the fun of learning only as a fourth-year student, when joining the lab of Professor Osamu Kurita (now professor at the Department of Administration Engineering) who was specializing in urban engineering and operations research and working on mathematical analysis of urban spaces. The way Prof. Kurita talked to us at the lab briefing was impressive. Particularly, his powerful analysis of various social problems using his wealth of knowledge as well as mathematical models was overwhelming. I was compelled to study under this professor. Even now I am still under the great influence of Prof. Kurita’s research style – mathematically approaching targets like urban and regional problems that have spatial structures.
But there were some tough aspects in my research life. It was because our lab had the policy of emphasizing the process in which students need to find their own research themes. As a student barely entering a research life, I had many difficulties. After all, for my graduation thesis I created a model to determine the optimal location of railway stations by focusing on access to the station. In retrospect, I cannot say it was a research work of high quality. I had a hard time setting the theme through trial and error but somehow developed a model from zero. This hard-earned experience was the origin of my career as a researcher, which remains a fond memory even today.
In reality, what structures to focus on varies according to the individual researcher. As such, the work of modeling inevitably involves the person’s subjectivity. No wonder modeling is often referred to as “art & science.” To put it another way, the fun of modeling lies in that each completed model contains some artistic elements that reflect the creator’s view of the world. Given that human or social problems are not governed by strict laws as in the world of physics, coexistence of multiple, dissimilar models is acceptable. For me, this was another intriguing aspect of this discipline. For a while during my master course years, I experienced internship at a think tank, which made me feel at a loss whether I should find employment there or not. But I finally decided to continue research work and enrolled in the doctoral course, remaining under the guidance of Prof. Kurita.
Returning to Keio after teaching at Tokyo University of Science and The Üniversity of Electro-Communications
After graduation from Keio, what experiences did you acquire?
After completing the doctoral course in March 2005, I became a research associate at Tokyo University of Science (TUS) in April. At TUS, I belonged to the Department of Management Science, Faculty of Engineering that covers disciplines similar to those of Keio. I had important experiences at TUS – guiding students in their graduation theses in addition to teaching exercises in mathematics and computer-based experimental courses. Then, in October 2008, I moved to The University of Electro-Communications (UEC). It was around that time that I was blessed with a son, three of us living together near the campus. During that period I devoted myself to research at UEC. So the years with UEC were when I tackled research themes that constitute the cores of my current work. Indeed, new ideas for research I conceived then turned to be a great asset for what I am doing now.
After five and a half years of teaching and research activities at UEC, I returned to Keio in 2014.
What is the current organization of your lab?

Established only three years ago, my lab has a modest number of member students: two master-course first year and five undergraduate students. Our policy here is to allow the students to proactively address themes they have found interesting. Naturally, their research themes range very widely, from a problem for ranking sports teams to mathematical analysis of cityscapes. They appear excited about approaching diverse social problems by developing mathematical models. When it comes to themes brought in by students, it is often the case that I also need to join them and rack our brains together, which in turn is another opportunity for me to learn anew and can lead to new discoveries.
How do you spend your days off?
My family consists of four members – a son who is an elementary school second grader, a daughter turning two years of age soon, my wife and myself. Maybe due to my influence, my son likes insect hunting (Laughter), impatiently looking for the summer vacation. My daughter seems to like singing, dancing and “Anpanman”. Recently she is becoming able to speak more and more words, which makes me happy. Going to aquariums and museums together and making trips are pleasant refreshers. My family is a source of my power.
Especially, my wife, who works as an editor for an academic publishing company, is a good adviser for me. She is originally from a law faculty and often offers useful advice on my new research themes because my studies mostly concern social problems. If I fail to make my wife understand my points, my research work is bound to go nowhere (Laughter). Don’t you think so?
What do you think are the merits of Keio University?
Actually there are many. But especially I’d like to point out the fact that both the teaching staff and students maintain a strong attachment to the Keio organization. It’s wonderful to find everyone always aware of and practicing the calls: “Keio should deliver impactful research results to the world” and “What should be done to make Keio an even better organization?”
Speaking of the Faculty of Science and Technology overall, it has an atmosphere of supporting young people. The whole faculty is willing to support young researchers in terms of research funds and opportunities for studying overseas. The strong feeling of unity and identity is the source of strength for Keio.
Some words from students
Student : Whatever questions we ask, Dr. Tanaka always responds sincerely and kindly with easy-to-understand answers. He is a really good teacher. Dr. Tanaka’s scope of knowledge is extremely wide, meaning he has many topics to talk about. What we can learn from Dr. Tanaka seems endless.
(Reporter & text writer: Madoka Tainaka)


