- Home
- New Kyurizukai
- Studies on Problem Solution
from Keio's Faculty of Science and Technology
Studies on Problem Solution
from Keio's Faculty of Science and Technology
The attraction ofOperations Research
– a scientific approach to solve“Problems” of the world.
Hoping to create a wide range of use of OR for society
Ms. Takeda is an active specialist in optimization, a field of Operations Research (OR) based on applied mathematics. However, on the contrary, she said that as a little girl she did rather poorly at school and studying was her weak point. But she used this inferiority complex to persevere in her great efforts to study and to maintain her spirit of inquiry, which paved the way for her to becoming a research scientist. However, no excitement can be seen behind her soft smiles. Instead of confining herself within the academic world, she appears always open-minded and outgoing, as she is willing to make her research results widely available to society.
Akiko Takeda
Ms. Takeda engages in the development of optimization techniques that take uncertainty factors into account. She addresses the development of algorithms for efficiently solving optimization problems in fields such as financial engineering and statistical machine learning. After obtaining the degree of Doctor of Science in 2001, she joined Toshiba Corporation’s R&D Center as a staff researcher. She then became Assistant Professor at Tokyo Institute of Technology’s Graduate School of Information Science and Engineering. From 2008 to present, she serves as Assistant Professor at Keio University’s Faculty of Science and Technology.
Introducing Researchers
Featured in this issue is Assistant Professor Akiko Takeda who challenges complex problems of our society, taking advantage of Operations Research (OR) techniques.
Using OR to Derive Optimal Solutions
Mathematics takes up the challenge of the actual world
Suppose you intend to reach your destination in a metropolitan area using different modes of public transportation such as JR, private and subway lines, you may be familiar with several different routes but may be at a loss which route to choose. In this type of case, the “train transfer guide” site accessible from your cellular phone or PC is very useful. Capable of instantly receiving the shortest and cheapest route from among the various routes, this convenient tool is the result of a field of applied mathematics known as Operations Research. What type of study is this OR that is inseparable from daily and vital needs of our modern society and Ms. Akiko Takeda’s specialty OR field?
What is Operations Research?
Ms. Akiko Takeda, Assistant Professor, Department of Administration Engineering, Keio University Fac u lty o f S c i e n c e a n d Technology, remarks: “Operations Research is a scientific method to find solutions to various problems of our world, taking advantage of mathematical and statistical modeling, statistics, algorithms and the like. I especially specialize in studies on what is known as “optimization” – a method of computation for problem solving. In this method, you model a targeted actual problem in the form of an optimization problem and seek a solution for the model. And the concept of “optimization” is concerned with diverse fields of applied studies, such as business management, finance, bioinformatics and control.” Operations Research is a field of study initiated during the Second World War (see the column on page 8). After the war ended, OR has made phenomenal progress in pace with the development of computers, and is now quantitatively utilized as an effective tool for solving complex and difficult problems of our society.
“For example, OR is used to compute solutions to questions such as “How many windows should a hospital or bank provide?” and “How long will an average waiting time be if the number of windows is pre-fixed?” Aside from the main issue, it may interest you to know that the current Prime Minister Yukio Hatoyama’s specialty was also OR when he was young and the theme of his doctoral thesis was ‘Machinery maintenance model based on the queuing theory.’ In other words, he studied the computing method as to at what point of time should machinery maintenance and repair be conducted.
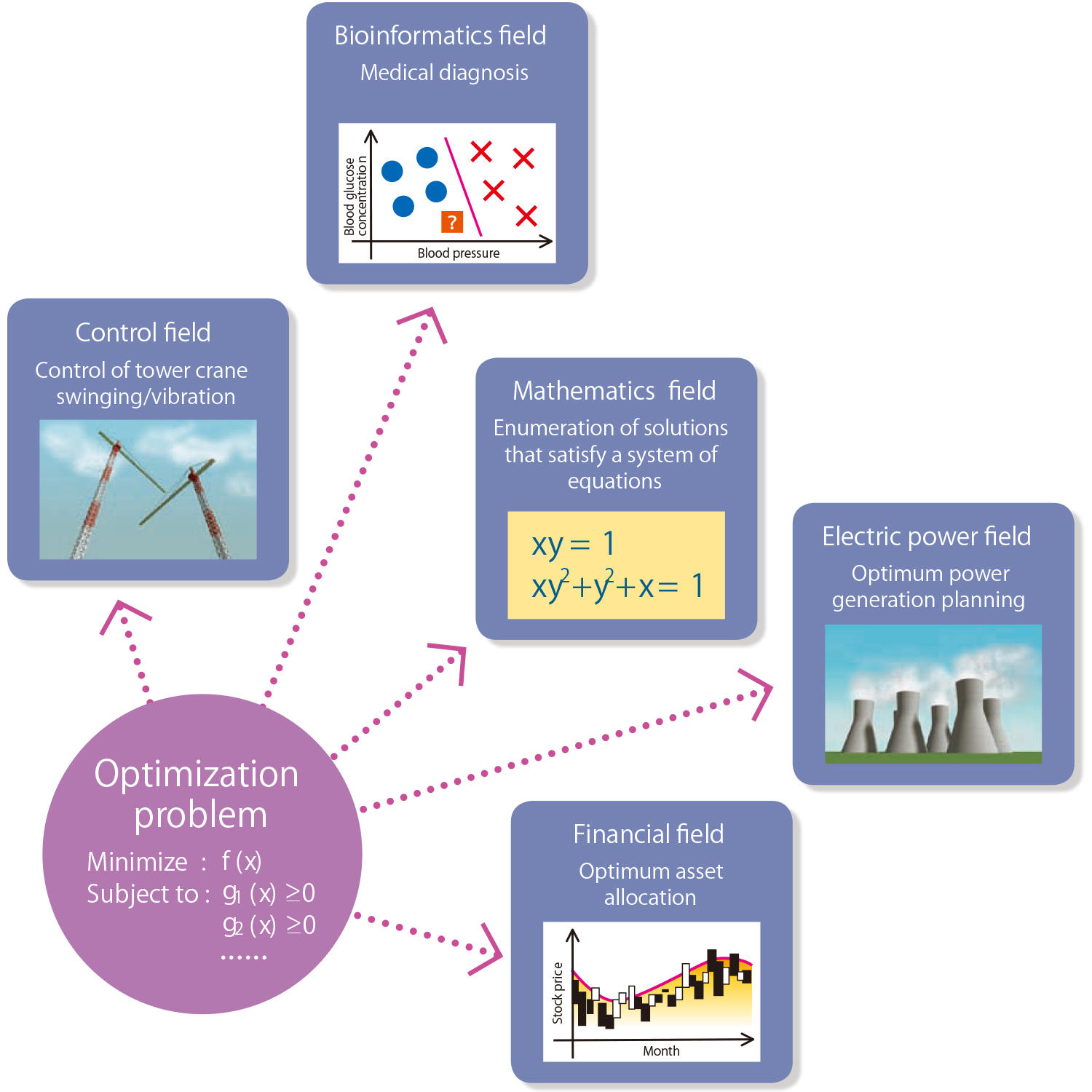
Optimization being applied to diverse fields
Upon completion of her doctor’s course, Ms. Takeda joined an electrical machinery manufacturer where she was assigned to a post tasked with power generation planning for an electric power company. The power c o m p a n y w o u l d utilize coal, oil, and natural gas-fueled generators and Ms. Takeda’s task was to determine power output for each of these generators so that the company c o u l d g e n e r a t e electricity at the lowest possible costs. It was a highly demanding task especially as it involved future fuel price changes due to foreign exchange rate fluctuations. She added: “Satisfying electricity needs was imperative as power failure was out of the question. At the same time I had to hold down costs while taking future fuel price fluctuations into account. However, solving the problem would become impossible if unforeseeable rapid price fluctuations had to be assumed. So it was required to set conditions within a solvable range.”
“Not limited to this problem, but after actually having solved problems, in most cases you find that the answers derived via OR are close or similar to what you have been practicing by rule of thumb at your workplace. However, you can use optimization as an effective means for obtaining a consensus within your company or persuading your client because it allows you to derive answers quantitatively instead of relying on intuition or experience. In recent times the optimization method is being increasingly used as a quantitative method to justify managerial choices.”
Furthermore, optimization is useful when examining and building up an investment portfolio based on an ideal combination of various financial products such as stocks, bonds, etc. It helps you to determine optimal asset allocation percentages to realize an expected level of return while minimizing risks as it allows you to combine issues prone to move according to market price fluctuations with those which are significantly less impacted by business trends.
Worthy of mention in this connection is Dr. Harry M. Markowitz who advocated a modern portfolio selection theory. He was awarded the Nobel Prize in Economic Sciences for his contribution of proposing a portfolio optimization problem known as the “Mean-Variance Model.”
Much is expected of Robust Optimization
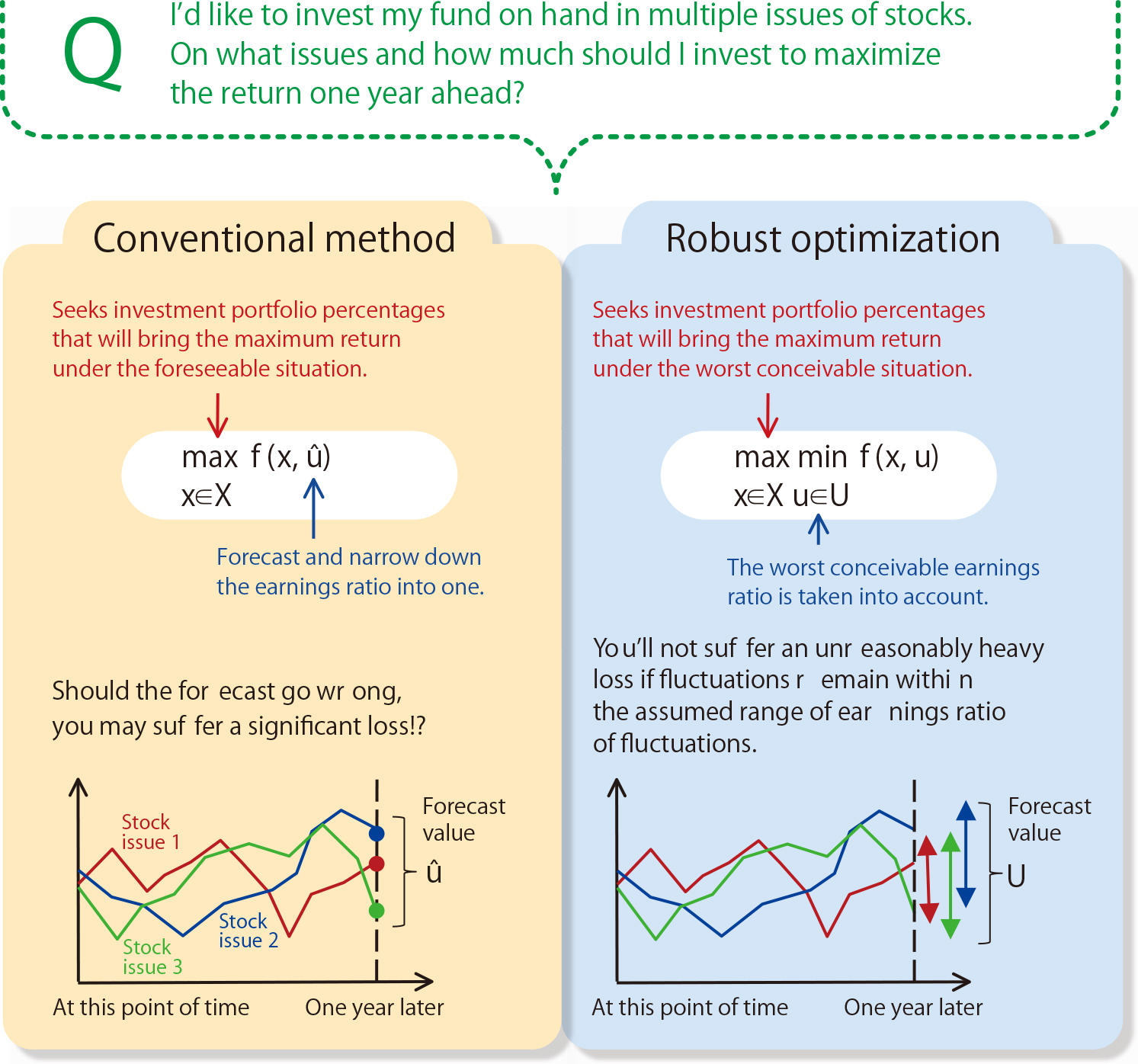
Meanwhile, optimization has its own problem. In the event of rapid stock price and/or foreign exchange fluctuations as seen in the recent economic turbulence triggered by the so-called “Lehman’s Shock,” investment portfolios, which were initially designed for low risk and high return by anticipating price/foreign exchange earnings ratios beforehand, often fail to match the market reality, making investors suffer significant losses. Although an optimization problem is created with the aim of building up a lowrisk/high-return portfolio, it becomes extremely difficult to apply the model to market reality if one single optimization problem is to be chosen by forecasting data such as earnings ratios.
As in the previous case of the generators at the electric power company, for example, answers will var y largely depending on how you forecast fuel pr ice f luc tuat ions. In t radit iona l m e t h o d o l o g i e s , w e d e f i n e d a n optimization problem by forecasting only one fuel price and derived the answer (which fuel-type generator to choose) despite the fact that fuel price is an uncertain factor. Should the forecast go wrong, reliability of the answer is lost. Against such a background, in 1998 two American research scientists, Aharon Ben-Tal and Arkadi Nemirovski, proposed what is known as the “Robust Optimization.” Instead of limiting data to only one since the data may be uncertain, this method offers a permissible range that allows you to derive the best possible answer to choose from while assuming the worst situation within the given range.
“While the term ‘robust’ means ‘strong’ or ‘tough,’ the robust optimization may be considered a method to derive a solution resistant to fluctuations. Back to the above-mentioned power generators, robust optimization enables the worst case to be anticipated as it makes computation by allowing some latitude for values concerning fuel price and electricity demand. This helps you when you make the actual decision.”
Robust optimization is also useful for optimization for tower crane operation to haul up an object. It optimizes the operation while allowing latitude for the object’s weight, the length of the crane’s rope and the arm’s boom’s angle as well as wind velocity which is an uncertain external force. Expectations are high for robust optimization as a tool that can maximize efficiency while satisfying the absolute requirement, safety.
“With robust optimization it is necessary to solve optimization problems of complex structure, but it is often the case that these problems are too difficult to obtain answers. This has given rise to a new wave of studies: “If yours is a robust optimization problem that satisfies a condition like this, then there is a way to transform it into an easier-to-handle problem”. This approach aims to answer how you can transform your problem into an easier one by satisfying such-andsuch conditions, or, if it’s impossible, what computation method should be employed to seek a relatively better answer instead of the ‘best possible’ answer.”
There are many themes of study for me to address. While theoretically solving these themes one by one, I would like to use the results of my work for the benefit of our society by expanding the scope of application through collaboration with research scientists from other diverse fields. Right now I’m writing a finance-related thesis, citing the robust optimization, along with one on machine learning related to bioinformatics.”
While in pursuit of mathematical theories, Ms. Takeda always pays attention to the real world. From Ms. Takeda’s work, I could recognize that Operations Research has unlimited potentialities and is indispensable as something that supports our modern society from behind the scenes.
Interview
Listening to what Assistant Professor Akiko Takeda says
A complete change from an elementary school dropout to a scientist
Our stereotype image of a mathematician is an extremely sharp and wise person. May I ask if you have been good at mathematics since your school days?

To tell you the truth, I was a dropout as an elementary school girl. I made the poorest grades in school – so bad that my mother was even called to the school and was asked why. (laughter) On top of that, I was like a tomboy, running around in the school, climbing trees in the schoolyard and so forth. I was always being scolded. Therefore, any one of my old friends in the elementary school days is surprised to hear that I’m now a research scientist. I’m truly thankful to my mother who told my teacher, “The problem about this girl is merely being slower than the other students in making progress.” This remark encouraged me and made me think that I would be OK only if I work harder than the others. There are a few reasons for my doing very poorly at school. Firstly, I was not very good at grasping the important points and was trying to study all the subjects to perfection but failed. Secondly, I was weak at subjects that required lot of memorizing. I didn’t remember mathematical formulas but instead tried to prove the formulas themselves during an exam and always ran out of time. As such, I had no favorite subjects until my high school days. All my high school classmates are surprised to hear that I chose a career as a mathematician. They unanimously say, “I thought you would go on to study liberal arts.” I might have been the type who did not want to lose at anything. I was so strong in a desire to overcome tough subjects that during my junior and senior high school days I strove to study all the subjects thoroughly, even subjects that required learning by memorization. Frankly speaking, I had no other choice than to continue studying mathematics, even though I did not particularly love it. (laughter) Maybe I just wanted to maintain a wide range of choice for my future. I don’t mean to praise myself, but I’m rather a hard-worker.
You mean you chose a career as a mathematician in the course of events as you continued striving? You didn’t have any special dream for the future or any special desire to do something?

As I recall, I didn’t have any particular coveted dream to become something. Incidentally, I was raised in a family background far from scientific studies: my father runs an apparel-related firm while both my younger sister and one of my cousins had been members of the Takarazuka Revue Company, singing and dancing until several years ago. So at the point of entering a university, the idea of becoming a scientist never occurred to me. Upon graduation from high school, I joined Keio University’s Faculty of Science and Technology where as a sophomore I chose the Department of Administration Engineering. In short, this department is where you study methodologies for creating and/or managing systems of society using mathematical tools. As such, targets of this learning have broad fields. Customer flow planning for supermarkets, production line planning for factories, and city planning . . . all these tasks are covered by the Department of Administration Engineering. Speaking of myself, I had specialized in mathematical economics through the master’s course. But soon I found myself increasingly intrigued by solving numerical formulas themselves. In fact, I became inclined for more mathematical studies, such as scheming out problem-solving methods and creating algorithms for packaging on computers and solving them. Under such circumstances, for the doctor’s course I moved to Tokyo Institute of Technology’s (TIT) Graduate School of Information Science and Engineering. I specialized in optimization, a field of operations research, and obtained the degree of Doctor of Science. Throughout the three years of the doctor’s course, I found myself absorbed in solving difficult problems. By that time I was inclined to see how my research results could be used to benefit the actual world. I was also interested in experiencing a life in the business world at least once. So, upon receiving my doctor’s degree I found employment with a major electric machinery manufacturer, where I was assigned to its laboratory to engage in optimization of generators for an electric power company.
Return to my alma mater after working as a scientist for an industrial company
Why did you return to TIT’s laboratory two years later?

My job at the electric machinery manufacturer was exciting and fulfilling because my clients were pleased with my work and I could see my research results leading to new products or patents. There was nothing to complain about. At the company’s laboratory I could discuss with my fellow researchers about each other’s research theme. But I sometimes felt a little lonely since I was assigned to do the job by myself and there was no one around me on the same professional level to discuss about my research theme. While I was allowed to continue my research work, the problem was that I was not permitted to write any theses freely due to patent-related reasons. Just two years after I joined the company, I was told, “Would you like to apply for a post of assistant at the Tokyo Institute of Technology? This will be the last chance for you to come back to TIT as a research scientist.” So I made up my mind to do so. Until then, I had not been confident enough to be able to establish myself as a researcher. I knew I was not the genius type. I also felt that I was not suited to pursue an academic career . . . I finally made up my mind to dedicate myself to study when I left the electric machinery manufacturer to return to the university. It was rather recently, only six to seven years ago. (laughter)
Then you moved again from the TIT’s laboratory to Keio University, right?
I returned to Keio two years ago. I got married around the time that I returned to the TIT’s laboratory that had a fixed term of service. Since my husband works as a research scientist for a university in Tokyo, my choice of workplace was limited to universities in the Tokyo Metropolitan area if I were to live with him under one roof. It was just about that time that Keio announced to publicly invite a researcher, for which I applied. I was more than happy when I was able to return to my alma mater, Keio.
Is your husband also engaged in studies similar to yours?
Yes, he is an OR research scientist like myself. I sometimes partner with him on a joint thesis. Some of my friends ask me, “Being a husband-and-wife team doing a joint thesis, don’t you quarrel?” Every time we quarrel, my husband always gives up. However, there’s a division of roles: as a specialist in financial engineering, my husband performs his role within his specialized field while I take charge of the theory side so we never quarrel. Right now we are working together on a joint thesis, which is in the finishing stage. We are positively stimulating each other even at home, often discussing about studies, asking for advice and so on.
It’s wonderful that the husband and wife can talk about studies while understanding each other’s work. By the way, what subjects are you now teaching at the university?
For sophomores and third-graders, I’m teaching OR, my specialty, in addition to mathematics. Also six seniors belong to my laboratory.
The TIT’s laboratory for which I had worked as an assistant is famous worldwide and there were many students in the doctor’s course as well as foreign students. But my own laboratory at Keio was established just recently and about half of my students will leave the campus as undergraduates. In this sense, my lab is still in the “preparation” stage, you might say. In short, I’m educating these students so that they will become able to properly write theses on their own and be able to conduct joint studies with me one day.
For those students eager to study for a period of three years including the master’s course, I give them the latest research themes while trying to have discussions on an ongoing basis. On the other hand, for students who will end their campus life as undergraduates, I’m trying to support them in matters of their interest so that they can enjoy studies.
A student who likes playing darts, for example, is engaged in study on optimization of darts as the extension of his hobby. When it comes to a student whose hobby is playing the flute, I encourage him to use the optimization technique to restore part of a musical score that was lost in war fire.
I’d like “optimization” to be known and used by more people
It’s possible to apply the optimization method of OR to such a diversity of areas, isn’t it? Very impressive!

Yes, indeed. That makes it interesting. I always want to maintain a wide range of choice just as I did as a student when going on to the university. In other words, I don’t want to limit my theories to only one application field. This is why I make it a rule to team up with people from many different fields according to research theme. It is true that mathematics contains areas of purely theoretical pursuit regardless of whether they can serve practical purposes of our society. In my case, however, I’m not happy unless I can see how theories are put into practical use, and how they can contribute to society. Theories without concrete applications have little appeal to me. Of course when teaming up with specialists from different specialties, there may be some conflict or friction due to the difference in academic cultures and areas of specialty, but that’s why it is interesting. Furthermore, I’d like to stress that only OR can offer quantitative advice for a business judgment that previously had only been dependent on intuition and experience. Yesterday, I heard from a fellow researcher that he persuaded a government official regarding their plan to reduce the number of cell phone base stations and that by using the optimization method, the minimum number of base stations that no radio wave interference would occur could be calculated. Optimization can be useful in such cases as well. Machine learning is one of my current research projects. I’m developing a machine learning method concerning the diagnosis of diabetes using Blood blood glucose concentration, insulin value and other data enabling judgment looking at such data and not having to depend only on the doctor’s diagnosis. As these examples indicate, the great attraction of the optimization method is that it not only allows us to enjoy mathematics but it can also be applied to various aspects of our modern society. I’d like to promote and let OR and optimization studies be better and widely known among more and more people so that they would say “Wow, I didn’t know optimization was used in such-and-such a thing!”
Just a word from . . .
A student : Ms. Takeda has a great power of concentration and often suddenly comes up with new ideas. On the other hand, she becomes almost blind to things other than the target that she is concentrating on. (laughter) She never fails to give advice whenever we ask her a question. She also always gives us new ideas one after another. She is always cheerful and optimistic so the lab’s atmosphere is always bright.
(Reporter & and text writer: Madoka Tainaka)


